3.5. Practice question answers

Ian Young; Aida Haghighi (editor)

Chapter 3 practice question answers

3.1. Introduction to Functions

1. Yes

2. No

3. Yes

4. Q = g(4) = 6

5. x = 0 or x = 2

6. a. g(5) = 1

b. m = 8

3.2. Domain and Range

1. Domain; y = years [1960,2010] ; Range, p = population, [100,1400]

2. a. Values that are less than or equal to -2, or values that are greater than or equal to -1 and less than 3

b. {x | x ≤ -2 or -1 ≤ x < 3}

c. (-∞, -2] ∪ [-1, 3)

3. Domain; y = years, [1952,2002] ; Range, p = population in millions, [40,88]

4. $T(c)=\begin{cases} 89.5c \quad if \quad c\le10\\ 895+33(c-10)\quad if \quad 10<c\le18 \quad Tuition,\;T,\;as\;a\;function\;of\;credits,\;c.\\ 1159+73(c-18)\quad if \quad c>18\\ \end{cases}$

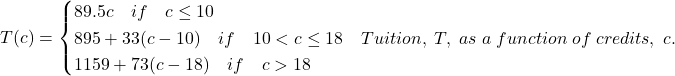
A reasonable domain should be whole numbers 0 to (answers may vary), e.g. [0,23]. A reasonable range should be $0 – (answers may vary), e.g. [0,1524].

5. a. {x | 2008 ≤ x ≤ 2018}, [2008, 2018]

b. {x | 16.1 ≤ x ≤ 88.4}, [16.1, 88.4]

3.3. Rates of Change and Behaviour of Graphs

1. $0.264 dollars per year.

2. Average rate of change = $\frac{1}{2}$ .

3. $\3a^2+3ah+h^2$

4. Based on the graph, the local maximum appears to occur at (-1, 28), and the local minimum occurs at (5,-80). The function is increasing on (-∞, -1)∪(5, ∞) and decreasing on (-1, 5).

5. a. -0.59 per 100,000

b. 6

c. 2010, 2014, and 2017

3.4. Quadratic Functions

1. $g(x)=x^2-6x+13$ in standard form; $g(x)=(x-3)^2+4$ in vertex form.