Exponents

Exponent review:  an or BaseExponent

Exponential notation Example
Base     Exponent
an= a ∙ a ∙ a ∙ a … a 24 = 2 ∙ 2 ∙ 2 ∙ 2  = 16
Read “a to the nth” or “the nth power of a.” Read “2 to the 4th.”

 

Properties of exponents:

Name Rule Example
Product rule a^m\;a^n=a^{m+n} 2^3\;2^2=2^{3 + 2}=2^5=32
Quotient rule \frac{a^m}{a^n}=a^{m-n} \frac{y^4}{y^2}=y^{4-2}=y^2
Power rule (a^m)^n=a^{mn}

(a^m \cdot b^n)^p=a^{mp}\;b^{np}

(\frac{a^m}{b^n})^p=\frac{a^{mp}}{b^{np}}

 (x^3)^2=x^{3\cdot2}=x^6

(t^3 \cdot s^4)^2=t^{3 \cdot 2}\;s^{4 \cdot 2}=t^6\;s^8

(\frac{q^2}{p^4})^3=\frac{q^{2\cdot3}}{p^{4\cdot3}}=\frac{q^6}{p^{12}}
Negative exponent a-n a^{-n}=\frac{1}{a^n} 4^{-2}=\frac{1}{4^2}=\frac{1}{16}
\frac{1}{a^{-n}}=a^n \frac{1}{4^{-2}}=4^2=16
Zero exponent   a0 a^0=1 15^0=1
One exponent   a1 a^1=a 7^1=7   ,   1^{13}=1
Fractional exponent a^\frac{m}{n}=\sqrt[n]{a^m} 15^\frac{2}{3}=\sqrt[3]{15^2}

 

  • Product rule: when multiplying two powers with the same base, keep the base and add the exponents.

am an = am + n            an   or   BaseExponent

Example: 23 22 = (2 · 2 · 2) (2 · 2) = 25 = 32
Or 23 22 = 23 + 2 = 25 = 32 A short cut, am an = am + n

 

  • Quotient rule: when dividing two powers with the same base, keep the base and subtract the exponents.

\frac{a^m}{a^n}=a^{m-n}

Example: \frac{\bf2^4}{\bf2^2}=\frac{2\cdot2\cdot\bcancel{2\cdot2}}{\bcancel{2\cdot2}}=2^2=4
Or \frac{\bf2^4}{\bf2^2}=2^{4-2}=2^2=4 A short cut, \frac{a^m}{a^n}=a^{m-n}

This law can also show that why a0 = 1 (zero exponent a0):  \frac{a^2}{a^2}=a^{2-2}=a^0=1

 

  • Power rule: when raising an expression to a power, we multiply each exponent inside the parentheses by the power outside the parentheses.

(am)n = amn,        (am · bn)p = amp bnp,        (\frac{a^m}{b^n})^p=\frac{a^{mp}}{b^{np}}

Example: (43)2 = (43) (43) = (4 · 4 · 4) (4 · 4 · 4) = 46 = 4096
Or (43)2 = 43 ∙ 2 = 46 = 4096 A short cut, (am)n = amn
Example: (2 · 3)2 = (2 · 3) (2 · 3) = 6 ∙ 6 = 36
Or (2 · 3)2 = 22 32 = 4 ∙ 9 = 36 A short cut , (a · b)n = an bn
Example: (\frac{2^2}{3^4})^3=(\frac{2^2}{3^4})(\frac{2^2}{3^4})(\frac{2^2}{3^4})=\frac{4\cdot4\cdot4}{81\cdot81\cdot81}=\frac{64}{531441}
Or (\frac{2^2}{3^4})^3=\frac{2^{2\cdot3}}{3^{4\cdot3}}=\frac{2^6}{3^{12}}=\frac{64}{531441} A short cut, (\frac{a^m}{b^n})^p=\frac{a^{mp}}{b^{np}}

 

  • Negative exponent: a negative exponent is the reciprocal of the number with a positive exponent.

a^{-n}=\frac{1}{a^n},  \frac{1}{a^{-n}}=a^n              a−n is the reciprocal of an.

Example: 3^{-4}=\frac{1}{3^4}=\frac{1}{81} a^{-n}=\frac{1}{a^n}
Example: \frac{1}{3^{-4}}=3^4=81 \frac{1}{a^{-n}}=a^n

 

  • Fractional exponent: a fractional exponent is a different way of writing a radical (i.e. root) sign. The base is first taken to the exponent of m, then the nth root is found to obtain the power.

a^{\frac{m}{n}} = {\sqrt[n]{a}^{m}} = {\sqrt[n]{a^{m}}}

Example: 5^{\frac{3}{2}} = {\sqrt[2]{5}^{3}} = {\sqrt[2]{5^{3}}} a^{\frac{m}{n}} = {\sqrt[n]{a^{m}}}

 

Example 1.5.1

Simplify (do not leave negative exponents in the answer).

1) {\bf (-4)^1}=-4 a^1=a
2) {\bf (-2345)^0}=1 a^0=1
3) {\bf x^2x^3}=x^{2+3}=x^5 a^m\;a^n=a^{m+n}
4) {\bf \frac{y^6}{y^4}}=y^{6-4}=y^2 \frac{a^m}{a^n}=a^{m-n}
5) {\bf (x^4)^{-3}}=x^{4(-3)}=x^{-12}=\frac{1}{x^{12}} (a^m)^n=a^{mn}  ,  \frac{1}{a^{-n}}=a^n
6) {\bf 7b^{-1}}=7\cdot \frac{1}{b^1}=\frac{7}{b} a^{-n}=\frac{1}{a^n}  ,  a^1=a
7) {\bf (2t^3\cdot w^2)^4}=2^4 t^{3\cdot4}\cdot w^{2\cdot4}=16t^{12} w^8 (a^m \cdot b^n)^p=a^{mp}\;b^{np}
8) {\bf \frac{1}{3^{-2}}}=3^2=9 \frac{1}{a^{-n}}=a^n
9) {\bf \frac{7x^4y^{-5}}{9^0\cdot x^2y^3}}=\frac{7x^{4-2}y^{-5-3}}{1}=7x^2y^{-8}=\frac{7x^2}{y^8} a^0=1  ,  \frac{a^m}{a^n}=a^{m-n}  ,  a^{-n}=\frac{1}{a^n}
10) {\bf (\frac{e^{-3}f^2}{g^{-2}})^{-2}}=\frac{e^{(-3)(-2)}f^{2(-2)}}{g^{(-2)(-2)}}=\frac{e^6f^{-4}}{g^4}=\frac{e^6}{g^4f^4} (\frac{a^m}{b^n})^p=\frac{a^{mp}}{b^{np}}  ,  \frac{1}{a^{-n}}=a^n

                   

 Simplifying Exponential Expressions

  • Remove parentheses using “power rule” if necessary.             (am bn)p = amp bnp
  • Regroup coefficients and variables.
  • Use “product rule” and “quotient rule”.                                   am an = am + n , \frac{a^m}{a^n}=a^{m-n}
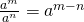
  • Simplify.
  • Use the “negative exponent” rule to make all exponents positive if necessary.

 

Example 1.5.2

Simplify.

1) \bf (3x^3y^2)^2 (2x^{-3}y^{-1})^3 (-248z^{-19})^0
=3^2x^{3\cdot2}y^{2\cdot2} \cdot 2^3x^{-3\cdot3} \cdot y^{-1\cdot3}\cdot1 Remove brackets. (\frac{a^m}{b^n})^p=\frac{a^{mp}}{b^{np}} , a^0=1
=(3^2\cdot2^3)(x^6x^{-9})(y^4y^{-3}) Regroup coefficients and variables.
=72x^{-3}y^1 Simplify. a^m\;a^n=a^{m+n}
=\frac{72y}{x^3} Make exponent positive. a^{-n}=\frac{1}{a^n} , a^1=a
2) \bf (\frac{(2x^4)(y^5)}{3x^3y^2})^2 (\frac{a^m}{b^n})^p=\frac{a^{mp}}{b^{np}}
=\frac{(2x^4)^2(y^5)^2}{(3x^3y^2)^2}
=\frac{2^2x^{4\cdot2}y^{5\cdot2}}{3^2x^{3\cdot2}y^{2\cdot2}} Remove brackets. (a \cdot b)^n=a^n\;b^n
=\frac{4}{9}\cdot \frac{x^8}{x^6}\cdot \frac{y^{10}}{y^4} Regroup coefficients and variables.
=\frac{4}{9}x^2y^6 Simplify. \frac{a^m}{a^n}=a^{m-n}

 

Example 1.5.3

Evaluate for   a = 2,   b = 1,   c = -1.

1) {\bf (-29a^{-5}b^4c^{-7})^0}=1 a^0=1
2) {\bf (\frac{a}{b})^{-4}}=(\frac{2}{1})^{-4} Substitute 2 for a and 1 for b,
=\frac{2^{-4}}{1^{-4}}=\frac{1^4}{2^4}=\frac{1}{16} \frac{a^m}{a^n}=a^{m-n}  ,  a^{-n}=\frac{1}{a^n}  ,  \frac{1}{a^{-n}}=a^n
3) {\bf (a+b-c)^a}=[2+1-(-1)]^2=4^2=16 Substitute 2 for a and 1 for b, and -1 for c.

Scientific Notation

Scientific notation is a special format to concisely express very large and small numbers.

Example:

300,000,000 = 3 × 108 m/sec. The speed of light.

0.00000000000000000016 = 1.6 × 10-19 C. An electron.

 

Scientific notation: a product of a number between 1 and 10 and a power of 10.

Scientific notation Example
N × 10±n 1 ≤ N < 10 67504.3 = 6.75043 × 104
n – integer Standard form Scientific notation

 

Writing a number in scientific notation:

Step Example
  • Move the decimal point after the first nonzero digit.

0.0079                  37213000
  • Determine n (the power of 10) by counting the number of places you moved the decimal.

n = 3                     n = 7
  • If the decimal point is moved to the right: × 10–n

0.0079 = 7.9 × 10-3

3 places to the right.
  • If the decimal point is moved to the left: × 10n

37213000. = 3.7213 × 107

7 places to the left.

 

Example 1.5.4

Write in scientific notation.

1)     2340000 = 2340000. = 2.34× 106

6 places to the left, × 10n

2)     0.000000439 = 4.39 × 10-7

7 places to the right, × 10-n

 

Example 1.5.5

Write in standard (or ordinary) form.

1)     6.4275 × 104 = 64275

2)     2.9 × 10-3 = 0.0029

 

Practice questions

1. Evaluate:

a. 4x2 + 5y,    for x = 1,    y = 4

b. (2a)3 – 3b,    for a = 5,    b = 6

2. Simplify (do not leave negative exponents in the answer):

a. (-92)1

b. y4 y3

c. \frac{x^9}{x^6}

d. 13a-1

e. (3a2 · b3)4

f. \frac{5x^5y^{-6}}{11^0x^3y^4}

g. (\frac{u^{-2}v^3}{w^{-4}})^{-3}       

3. Write in scientific notation:

a. 45,600,000

b. 0.00000523

4. Write in standard (or ordinary) form:

a. 3.578 × 103

b. 4.3 × 10-5

 

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Mathematics for Public and Occupational Health Professionals Copyright © 2019 by Ian Young is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.