2.4. Applications

Ian Young

2.4. Applications

Applications

Now that we have learned to determine equations of lines, we can apply these ideas to real-life equations.

Example 2.4.1

A taxi service charges $0.50 per mile plus a $5 flat fee. What will be the cost of traveling 20 miles? What will be cost of traveling x miles?

Solution

The cost of traveling 20 miles = y = (.50)(20) + 5 = 10 + 5 = 15

The cost of traveling x miles = y = (.50)(x) + 5 = .50x + 5

In the above problem, $0.50 per mile is referred to as the variable cost, and the flat charge $5 as the fixed cost. Now if we look at our cost equation y = .50x + 5, we can see that the variable cost corresponds to the slope and the fixed cost to the y-intercept.

Example 2.4.2

The variable cost to manufacture a product is $10 and the fixed cost $2500. If x represents the number of items manufactured and y the total cost, write the cost function.

Solution

The variable cost represents the slope and the fixed cost represents the y-intercept. Therefore, m = 10 and y = 2500.

The cost equation is y = 10x + 2500.

Example 2.4.3

It costs $750 to manufacture 25 items, and $1000 to manufacture 50 items. Assuming a linear relationship holds, find the cost equation, and use this function to predict the cost of 100 items.

Solution

We let x = the number of items manufactured, and let y = the cost.

Solving this problem is equivalent to finding an equation of a line that passes through the points (25, 750) and (50, 1000).

$m=\frac{1000-750}{50-25}=10$

Therefore, the partial equation is y = 10x + b.

By substituting one of the points in the equation, we get b = 500.

Therefore, the cost equation is y = 10x + 500.

Now to find the cost of 100 items, we substitute x = 100 in the equation y = 10x + 500.

So the cost = y = 10(100) + 500 = 1500.

Example 2.4.4

The freezing temperature of water in Celsius is 0 degrees and in Fahrenheit 32 degrees. And the boiling temperatures of water in Celsius, and Fahrenheit are 100 degrees, and 212 degrees, respectively. Write a conversion equation from Celsius to Fahrenheit and use this equation to convert 30 degrees Celsius into Fahrenheit.

Solution

Let us look at what is given.

Centigrade	Fahrenheit
0	32
100	212

Again, solving this problem is equivalent to finding an equation of a line that passes through the points (0, 32) and (100, 212).

Since we are finding a linear relationship, we are looking for an equation y = mx + b, or in this case F = mC+ b, where x or C represent the temperature in Celsius, and y or F the temperature in Fahrenheit.

slope $m=\frac{212-32}{100-0}=\frac{9}{5}$

The equation is $F=\frac{9}{5}C+b$

Substituting the point (0, 32), we get

$F=\frac{9}{5}C+32$

Now to convert 30 degrees Celsius into Fahrenheit, we substitute C = 30 in the equation

$F=\frac{9}{5}C+32$

$F=\frac{9}{5}(30)+32=86$

Example 2.4.5

The population of Canada in the year 1970 was 18 million, and in 1986 it was 26 million. Assuming the population growth is linear, and x represents the year and y the population, write the function that gives a relationship between the time and the population. Use this equation to predict the population of Canada in 2010.

Solution

The problem can be made easier by using 1970 as the base year, that is, we choose the year 1970 as the year zero. This will mean that the year 1986 will correspond to year 16, and the year 2010 as the year 40.

Now we look at the information we have.

Solving this problem is equivalent to finding an equation of a line that passes through the points (0, 18) and (16, 26).

$m=\frac{26-18}{16-0}=\frac{1}{2}$

The equation is $y=\frac{1}{2}x+b$ .

Substituting the point (0, 18), we get:

$y=\frac{1}{2}x+18$

Now to find the population in the year 2010, we let x = 40 in the equation:

$y=\frac{1}{2}x+18$

$y=\frac{1}{2}(40)+18=38$

So the population of Canada in the year 2010 is estimated as 38 million.

Year	Population
0 (1970)	18 million
16 (1986)	26 million

More Applications

In this section, you will learn to:

Solve a linear system in two variables.
Find the equilibrium point when a demand and a supply equation are given.
Find the break-even point when the revenue and the cost functions are given.

In this section, we will do application problems that involve the intersection of lines. Therefore, before we proceed any further, we will first learn how to find the intersection of two lines.

Example 2.4.6

Find the intersection of the line y = 3x − 1 and the line y = −x + 7.

Solution

We graph both lines on the same axes, as shown below, and read the solution (2, 5).

Finding the intersection of two lines graphically is not always easy or practical; therefore, we will now learn to solve these problems algebraically.

At the point where two lines intersect, the x and y values for both lines are the same. So in order to find the intersection, we either let the x-values or the y-values equal.

If we were to solve the above example algebraically, it will be easier to let the y-values equal. Since y = 3x − 1 for the first line, and y = −x + 7 for the second line, by letting the y-values equal, we get:

$3x-1=-x+7$

$4x = 8$

$x = 2$

By substituting x = 2 in any of the two equations, we obtain y = 5. Hence, the solution (2, 5).

One common algebraic method used in solving systems of equations is called the elimination method. The object of this method is to eliminate one of the two variables by adding the left and right sides of the equations together. Once one variable is eliminated, we get an equation that has only one variable for which it can be solved. Finally, by substituting the value of the variable that has been found in one of the original equations, we get the value of the other variable. The method is demonstrated in the example below.

Example 2.4.7

Find the intersection of the lines 2x + y = 7 and 3x − y = 3 by the elimination method.

Solution

We add the left and right sides of the two equations.

$2x + y = 7$

$3x-y = 3$

$5x = 10$

$x = 2$

Now we substitute x = 2 in any of the two equations and solve for y.

$2(2)+y=7$

$y = 3$

Therefore, the solution is (2, 3).

Example 2.4.8

Solve the system of equations x + 2y = 3 and 2x + 3y = 4 by the elimination method.

Solution

If we add the two equations, none of the variables are eliminated. But the variable x can be eliminated by multiplying the first equation by -2, and leaving the second equation unchanged.

$-2x-4y=-6$

$2x+3y=4$

$-y=-2$

$y = 2$

Substituting y = 2 in x + 2y = 3, we get

$x+2(2) = 3$

$x =-1$

Therefore, the solution is (-1, 2).

Example 2.4.9

Solve the system of equations 3x − 4y = 5 and 4x − 5y = 6.

Solution

This time, we multiply the first equation by -4 and the second by 3 before adding. (The choice of numbers is not unique.)

$-12x + 16y =-20$

$12x-15y = 18$

$y =-2$

By substituting y = -2 in any one of the equations, we get x = -1. Hence the solution (-1, -2).

Supply, Demand and the Equilibrium Market Price

In a free market economy the supply curve for a commodity is the number of items of a product that can be made available at different prices, and the demand curve is the number of items the consumer will buy at different prices. As the price of a product increases, its demand decreases and supply increases. On the other hand, as the price decreases the demand increases and supply decreases. The equilibrium price is reached when the demand equals the supply.

Example 2.4.10

The supply curve for a product is y = 1.5x + 10 and the demand curve for the same product is y = -2.5x + 34, where x is the price and y the number of items produced. Find the following:

a. How many items will be supplied at a price of $10?

b. How many items will be demanded at a price of $10?

c. Determine the equilibrium price.

d. How many items will be produced at the equilibrium price?

Solution

a. We substitute x = 10 in the supply equation, y = 1.5x + 10, and the answer is y = 25.

b. We substitute x = 10 in the demand equation, y = -2.5x + 34, and the answer is y = 9.

c. By letting the supply equal the demand, we get:

$1.5x + 10 =-2.5x + 34$

$4x = 24$

$x = 6$

d. We substitute x = 6 in either the supply or the demand equation and we get y = 19. The graph below shows the intersection of the supply and the demand functions and their point of intersection, (6, 19).

Break-Even Point

In a business, profit is generated by selling products. If a company sells x number of items at a price P, then the revenue R is P times x , i.e., R = P · x. The production costs are the sum of the variable costs and the fixed costs, and are often written as C = mx + b, where x is the number of items manufactured.

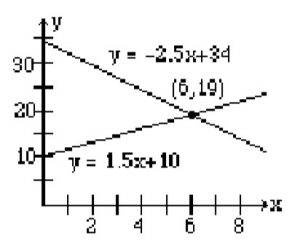
A company makes a profit if the revenue is greater than the cost, and it shows a loss if the cost is greater than the revenue. The point on the graph where the revenue equals the cost is called the break-even point.

Example 2.4.11

If the revenue function of a product is R = 5x and the cost function is y = 3x + 12, find the following:

a. If 4 items are produced, what will the revenue be?

b. What is the cost of producing 4 items?

c. How many items should be produced to break-even?

d. What will be the revenue and the cost at the break-even point?

Solution

a. We substitute x = 4 in the revenue equation R = 5x, and the answer is R = 20.

b. We substitute x = 4 in the cost equation C = 3x + 12, and the answer is C = 24.

c. By letting the revenue equal the cost, we get:

$5x = 3x+12$

$x=6$

d. We substitute x = 6 in either the revenue or the cost equation, and we get R = C = 30. The graph below shows the intersection of the revenue and the cost functions and their point of intersection, (6, 30).

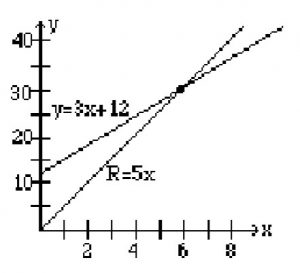
Practice questions

1. The variable cost to manufacture an item is $20, and it costs a total of $750 to produce 20 items. If x represents the number of items manufactured and y the cost, write the cost function.

2. A person who weighs 150 pounds has 60 pounds of muscles, and a person that weighs 180 pounds has 72 pounds of muscles. If x represents the body weight and y the muscle weight, write an equation describing their relationship. Use this relationship to determine the muscle weight of a person that weighs 170 pounds.

3. In 2005, an average house in Greater Toronto Area cost $335,907 and the average house in 2018 cost $787,300. Assuming a linear relationship, predict the price of a similar house in the year 2025.

4. In 2010 there were 11,386 laboratory-confirmed cases of gonorrhea reported in Canada. In 2015, the number of cases increased to 19,845. Assuming a linear relationship, how many cases of gonorrhea might we expect in 2030?

5. The supply curve for a product is y = 2000x + 13000, and the demand curve is y = -1000x + 28000, where x represents the price and y the number of items. At what price will the supply equal demand, and how many items will be produced at that price?

6. A company that produces toys has a fixed cost of $10,725, and variable cost of 20 cents a toy. Find the break-even point if the toys sell for $1.50 each.

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Mathematics for Public and Occupational Health Professionals Copyright © 2019 by Ian Young is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.