6.1. Sample Spaces and Probability

Ian Young

6.1. Sample Spaces and Probability

Sample Spaces and Probability

If two coins are tossed, what is the probability that both coins will fall heads? The problem seems simple enough, but it is not uncommon to hear the incorrect answer of $1/3$ . A student may incorrectly reason that if two coins are tossed there are three possibilities, one head, two heads, or no heads. Therefore, the probability of two heads is one out of three. The answer is wrong because if we toss two coins there are four possibilities and not three. For clarity, assume that one coin is a penny and the other a nickel. Then we have the following four possibilities:

HH HT TH TT

The possibility HT, for example, indicates a head on the penny and a tail on the nickel, while TH represents a tail on the penny and a head on the nickel.

It is for this reason, we emphasize the need for understanding sample spaces.

An act of flipping coins, rolling dice, drawing cards, or surveying people are referred to as an experiment.

Sample Spaces: A sample space of an experiment is the set of all possible outcomes.

Example 6.1.1

If a die is rolled, write a sample space.

Solution

A die has six faces each having an equally likely chance of appearing. Therefore, the set of all possible outcomes S is:

{1, 2, 3, 4, 5, 6}.

Example 6.1.2

A family has three children. Write a sample space.

Solution

The sample space consists of eight possibilities:

{BBB , BBG , BGB , BGG , GBB , GBG , GGB , GGG}

The possibility BGB, for example, indicates that the first born is a boy, the second born a girl, and the third a boy.

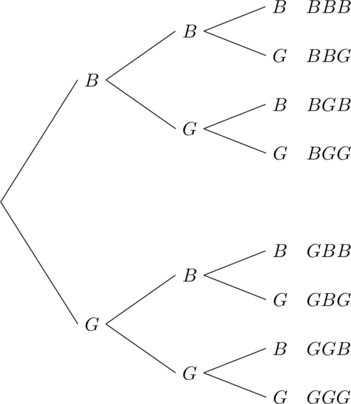
We illustrate these possibilities with a tree diagram:

Rendered by QuickLaTeX.com

Example 6.1.3

Two dice are rolled. Write the sample space.

Solution

We assume one of the dice is red, and the other green. We have the following 36 possibilities:

	Green
Red	1	2	3	4	5	6
1	(1, 1)	(1, 2)	(1, 3)	(1, 4)	(1, 5)	(1, 6)
2	(2, 1)	(2, 2)	(2, 3)	(2, 4)	(2, 5)	(2, 6)
3	(3, 1)	(3, 2)	(3, 3)	(3, 4)	(3, 5)	(3, 6)
4	(4, 1)	(4, 2)	(4, 3)	(4, 4)	(4, 5)	(4, 6)
5	(5, 1)	(5, 2)	(5, 3)	(5, 4)	(5, 5)	(5, 6)
6	(6, 1)	(6, 2)	(6, 3)	(6, 4)	(6, 5)	(6, 6)

The entry (2, 5), for example, indicates that the red die shows a two, and the green a 5.

Now that we understand the concept of a sample space, we will define probability.

Probability: For a sample space S, and an outcome A of S, the following two properties are satisfied.

If A is an outcome of a sample space, then the probability of A, denoted by P(A), is between 0 and 1, inclusive. 0 ≤ P(A) ≤ 1
The sum of the probabilities of all the outcomes in S equals 1.

Example 6.1.4

If two dice, one red and one green, are rolled, find the probability that the red die shows a 3 and the green shows a six.

Solution

Since two dice are rolled, there are 36 possibilities. The probability of each outcome, listed in Example 6.1.3, is equally likely. Since (3, 6) is one such outcome, the probability of obtaining (3, 6) is 1/36.

The example we just considered consisted of only one outcome of the sample space. We are often interested in finding probabilities of several outcomes represented by an event.

An event is a subset of a sample space. If an event consists of only one outcome, it is called a simple event.

Example 6.1.5

If two dice are rolled, find the probability that the sum of the faces of the dice is 7.

Solution

Let E represent the event that the sum of the faces of two dice is 7. Since the possible cases for the sum to be 7 are: (1, 6), (2, 5), (3, 4), (4, 3), (5, 2), and (6, 1).

E = {(1, 6), (2, 5), (3, 4), (4, 3), (5, 2), and (6, 1)}

and the probability of the event E:

P(E) = 6/36 or 1/6.

Example 6.1.6

A jar contains 3 red, 4 white, and 3 blue marbles. If a marble is chosen at random, what is the probability that the marble is a red marble or a blue marble?

Solution

We assume the marbles are r₁, r₂, r₃, w₁, w₂, w₃, w₄, b₁, b₂, b₃. Let the event C represent that the marble is red or blue.

The sample space S = {r₁, r₂, r₃, w₁, w₂, w₃, w₄, b₁, b₂, b₃}

And the event C = {r₁, r₂, r₃, b₁, b₂, b₃}

Therefore, the probability of C:

P(C) = 6/10 or 3/5.

Example 6.1.7

A jar contains three marbles numbered 1, 2, and 3. If two marbles are drawn, what is the probability that the sum of the numbers is 4?

Solution

Since two marbles are drawn, the sample space consists of the following six possibilities:

S = {(1, 2), (1, 3), (2, 3), (2, 1), (3, 1), (3, 2)}

Let the event F represent that the sum of the numbers is four. Then:

F = [(1, 3), (3, 1)]

Therefore, the probability of F is:

P(F) = 2/6 or 1/3.

Example 6.1.8

A jar contains three marbles numbered 1, 2, and 3. If two marbles are drawn, what is the probability that the sum of the numbers is at least 4?

Solution

The sample space, as in Example 6.1.7, consists of the following six possibilities:

S = {(1, 2), (1, 3), (2, 3), (2, 1), (3, 1), (3, 2)}

Let the event A represent that the sum of the numbers is at least four. Then:

F = {(1, 3), (3, 1), (2, 3), (3, 2)}

Therefore, the probability of F is:

P(F) = 4/6 or 2/3.

Practice questions

1. Write a sample space for the following event: a die is rolled, and a coin is tossed.

2. A card is selected from a deck of 52 playing cards. Find the following probabilities:

a. P (a king)

b. P (any suit other than hearts)

3. A jar contains 6 red, 7 white, and 7 blue marbles. If a marble is chosen at random, find the following probabilities:

a. P (red)

b. P (red or blue)

4. Two dice are rolled. Find the following probabilities:

a. P (the sum of the dice is 5)

b. P (the sum of the dice is 3 or 6)

5. A family has four children. Find the following probabilities:

a. P (they have two boys and two girls)

b. P (they have three or more girls)

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Mathematics for Public and Occupational Health Professionals Copyright © 2019 by Ian Young is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.