3.4. Quadratic Functions
Quadratic Functions
In this section, we will explore quadratic functions, a type of polynomial function. Quadratics commonly arise from problems involving areas, as well as revenue and profit, providing some interesting applications.
Example 3.4.1
A backyard farmer wants to enclose a rectangular space for a new garden. She has purchased 80 feet of wire fencing to enclose 3 sides, and will put the 4th side against the backyard fence. Find a formula for the area enclosed by the fence if the sides of fencing perpendicular to the existing fence have length L.
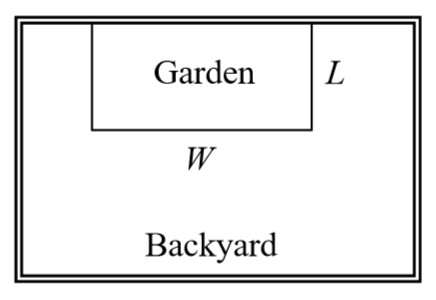
In a scenario like this involving geometry, it is often helpful to draw a picture. It might also be helpful to introduce a temporary variable, W, to represent the side of fencing parallel to the 4th side or backyard fence.
Since we know we only have 80 feet of fence available, we know that L + W + L = 80 , or more simply, 2L + W = 80 . This allows us to represent the width, W, in terms of L: W = 80 – 2L
Now we are ready to write an equation for the area the fence encloses. We know the area of a rectangle is length multiplied by width, so:
A = LW = L(80 – 2L)
A(L) = 80L – 2L2
This formula represents the area of the fence in terms of the variable length L.
Short Run Behaviour: Vertex
We now explore the interesting features of the graphs of quadratics. In addition to intercepts, quadratics have an interesting feature where they change direction, called the vertex.
The standard form for a quadratic is ![]() , but you will often see them written in the form
, but you will often see them written in the form ![]() . To see why, consider this example.
. To see why, consider this example.
Example 3.4.2
Sketch a graph of ![]() :
:
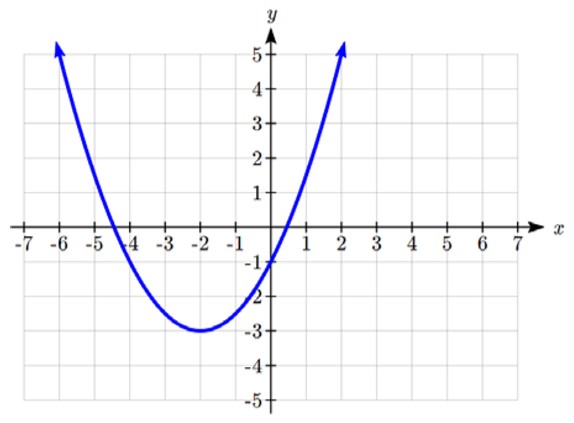
We can create a table of values, which we can use to plot several points and connect them with a smooth curve.
| x | g(x) |
| -5 | 1.5 |
| -4 | -1 |
| -3 | -2.5 |
| -2 | -3 |
| -1 | -2.5 |
| 0 | -1 |
| 1 | 1.5 |
Notice that the turning point of the graph, where it changes from decreasing to increasing, is at the point (-2, -3). We call this point the vertex of the quadratic. Notice that ![]() can also be written as
can also be written as ![]() . Comparing that to the form
. Comparing that to the form ![]() , you can see that the vertex of the graph, (-2, -3), corresponds with the point (h, k).
, you can see that the vertex of the graph, (-2, -3), corresponds with the point (h, k).
Forms of Quadratic Functions:
The standard form of a quadratic function is ![]() .
.
The vertex form of a quadratic function is ![]() .
.
The vertex of the quadratic function is located at (h, k), where h and k are the numbers in the vertex form of the function.
When a > 0, the graph of the quadratic will open upwards.
When a < 0, the graph of the quadratic will open downwards.
|
a > 0 |
a < 0 |
Example 3.4.3
Write ![]() in standard form.
in standard form.
To write this in standard polynomial form, we could expand the formula and simplify terms:
![]()
![]()
![]()
![]()
![]()
In the previous example, we saw that it is possible to rewrite a quadratic function given in vertex form and rewrite it in standard form by expanding the formula. It would be useful to reverse this process, since the transformation form reveals the vertex.
Finding the vertex of a quadratic: for a quadratic given in standard form, the vertex (h, k) is located at:
![]() ,
, ![]()
Example 3.4.4
Find the vertex of the quadratic ![]() . Rewrite the quadratic into vertex form.
. Rewrite the quadratic into vertex form.
The horizontal coordinate of the vertex will be at ![]()
The vertical coordinate of the vertex will be at ![]()
Rewriting into vertex form, the value of a will remain the same as in the original quadratic.
![]()
In addition to enabling us to more easily graph a quadratic written in standard form, finding the vertex serves another important purpose – it allows us to determine the maximum or minimum value of the function, depending on which way the graph opens.
Example 3.4.5
Returning to our backyard farmer from the beginning of the section, what dimensions should she make her garden to maximize the enclosed area?
Earlier we determined the area she could enclose with 80 feet of fencing on three sides was given by the equation A(L) = 80L – 2L2 . Notice that quadratic has been vertically reflected, since the coefficient on the squared term is negative, so the graph will open downwards, and the vertex will be a maximum value for the area.
In finding the vertex, we know that a is the coefficient on the squared term, so a = -2, b = 80, and c = 0.
Finding the vertex: ![]() ,
, ![]()
The maximum value of the function is an area of 800 square feet, which occurs when L = 20 feet. When the shorter sides are 20 feet, that leaves 40 feet of fencing for the longer side. To maximize the area, she should enclose the garden so the two shorter sides have length 20 feet, and the longer side parallel to the existing fence has length 40 feet.
Short run Behavior: Intercepts
As with any function, we can find the vertical intercepts of a quadratic by evaluating the function at an input of zero, and we can find the horizontal intercepts by solving for when the output will be zero. Notice that depending upon the location of the graph, we might have zero, one, or two horizontal intercepts.
 zero horizontal intercepts zero horizontal intercepts |
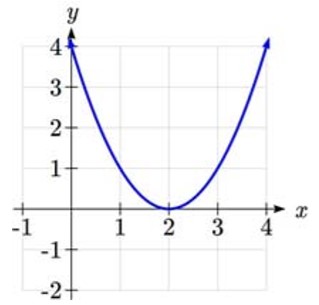 one horizontal intercept one horizontal intercept |
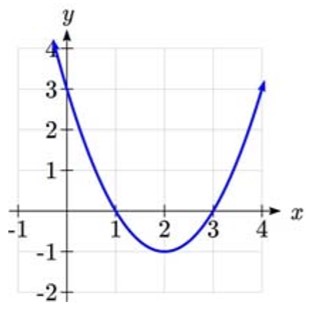 two horizontal intercepts two horizontal intercepts |
We can determine the vertical and horizontal intercepts of a quadratic using the quadratic formula.
Quadratic formula: for a quadratic function given in standard form ![]() , the quadratic formula gives the horizontal intercepts of the graph of this function.
, the quadratic formula gives the horizontal intercepts of the graph of this function.
![]()
Example 3.4.6
A ball is thrown upwards from the top of a 40 foot high building at a speed of 80 feet per second. The ball’s height above ground can be modeled by the equation
![]() .
.
What is the maximum height of the ball?
When does the ball hit the ground?
To find the maximum height of the ball, we would need to know the vertex of the quadratic.
![]()
The ball reaches a maximum height of 140 feet after 2.5 seconds.
To find when the ball hits the ground, we need to determine when the height is zero – when H(t) = 0. While we could do this using the transformation form of the quadratic, we can also use the quadratic formula:
![]()
Since the square root does not simplify nicely, we can use a calculator to approximate the values of the solutions:
![]() or
or ![]()
The second answer is outside the reasonable domain of our model, so we conclude the ball will hit the ground after about 5.458 seconds.
Example 3.4.7
The supply for a certain product can be modeled by ![]() and the demand can be modeled by
and the demand can be modeled by ![]() , where p is the price in dollars, and q is the quantity in thousands of items. Find the equilibrium price and quantity.
, where p is the price in dollars, and q is the quantity in thousands of items. Find the equilibrium price and quantity.
Recall that the equilibrium price and quantity is found by finding where the supply and demand curve intersect. We can find that by setting the equations equal:
![]() Add 2q2 to both sides
Add 2q2 to both sides
![]() Divide by 5 on both sides
Divide by 5 on both sides
![]() Take the square root of both sides
Take the square root of both sides
![]()
Since it doesn’t make sense to talk about negative quantities, the equilibrium quantity is q = 18. To find the equilibrium price, we evaluate either function at the equilibrium quantity.
![]()
The equilibrium is 18 thousand items, at a price of $972.
Practice questions
1. Write ![]() in standard form and then in vertex form.
in standard form and then in vertex form.
2. For these two equations determine if the vertex will be a maximum value or a minimum value.
a. ![]()
b. ![]()
3. Rewrite the following equation in vertex form: ![]() .
.
4. Jim has 32 m of fencing to surround a garden, bounded on one side by the wall of his house. What are the dimensions of the largest rectangular garden he can enclose?
5. A new start-up company has determined that their daily profits, P, from selling x boxes of N95 particulate respirator masks is given by: ![]() . In this scenario, what would be the company’s maximum daily profit?
. In this scenario, what would be the company’s maximum daily profit?
6. A ball is thrown from the top of a 35 m tall building at a speed of 24.5 m per second. The ball’s height above ground can be modelled by the equation: ![]() .
.
a. What is the maximum height of the ball?
b. When does it hit the ground?