5.3. Permutations

Ian Young

5.3. Permutations

Permutations

In a previous example, we were asked to find the word sequences formed by using the letters {A,B,C} if no letter is to be repeated. The tree diagram gave us the following six arrangements:

ABC, ACB, BAC, BCA, CAB, and CBA

Arrangements like these, where order is important and no element is repeated, are called permutations.

Permutations: A permutation of a set of elements is an ordered arrangement where each element is used once.

Example 5.3.1

How many three-letter word sequences can be formed using the letters {A, B, C, D}?

Solution

There are four choices for the first letter of our word, three choices for the second letter, and two choices for the third.

4

3

2

Applying the multiplication axiom, we get 4 · 3 · 2 = 24 different arrangements.

Example 5.3.2

How many permutations of the letters of the word ARTICLE have consonants in the first and last positions?

Solution

In the word ARTICLE, there are 4 consonants. Since the first letter must be a consonant, we have four choices for the first position, and once we use up a consonant, there are only three consonants left for the last spot. We show as follows:

4

3

Since there are no more restrictions, we can go ahead and make the choices for the rest of the positions. So far we have used up 2 letters, therefore, five remain. So for the next position there are five choices, for the position after that there are four choices, and so on. We get:

4

5

4

3

2

1

3

So the total permutations are 4 · 5 · 4 · 3 · 2 · 1 · 3 = 1440.

Example 5.3.3

Given five letters {A, B, C, D, E}. Find the following:

a. The number of four-letter word sequences.

b. The number of three-letter word sequences.

c. The number of two-letter word sequences.

Solution

The problem is easily solved by the multiplication axiom, and answers are as follows:

a. The number of four-letter word sequences is 5 · 4 · 3 · 2 = 120.

b. The number of three-letter word sequences is 5 · 4 · 3 = 60.

c. The number of two-letter word sequences is 5 · 4 = 20.

We often encounter situations where we have a set of n objects and we are selecting r objects to form permutations. We refer to this as permutations of n objects taken r at a time, and we write it as nPr.

Therefore, this example can also be answered as listed below:

a. The number of four-letter word sequences is 5P4 = 120.

b. The number of three-letter word sequences is 5P3 = 60.

c. The number of two-letter word sequences is 5P2 = 20.

Before we give a formula for nPr, we’d like to introduce a symbol that we will use a great deal in this as well as in the next chapter.

Factorial: n! = n(n − 1)(n − 2)(n − 3)··· 3 · 2 · 1.

Where n is a natural number.

0! = 1

Now we define nPr.

The Number of Permutations of n Objects Taken r at a Time:

nPr = n(n − 1)(n − 2)(n − 3)···(n − r +1), or

nPr = $\frac{n!}{(n-r)!}$

Where n and r are natural numbers.

The reader should become familiar with both formulas and should feel comfortable in applying either.

Example 5.3.4

Compute the following using both formulas.

a. 6P3

b. 7P2

Solution

We will identify n and r in each case and solve using the formulas provided.

a. 6P3 = 6 · 5 · 4 = 120, alternately 6P3 = $\frac{6!}{(6-3)!}$ = $\frac{6!}{3!}$ = $\frac{6\cdot5\cdot4\cdot3\cdot2\cdot1}{3\cdot2\cdot1}$ = 120

b. 7P2 = 7 · 6 = 42, or 7P2 = $\frac{7!}{5!}$ = $\frac{7\cdot6\cdot5\cdot4\cdot3\cdot2\cdot1}{5\cdot4\cdot3\cdot2\cdot1}$ = 42

Next we consider some more permutation problems to get further insight into these concepts.

Example 5.3.5

In how many different ways can 4 people be seated in a straight line if two of them insist on sitting next to each other?

Solution

Let us suppose we have four people A, B, C, and D. Further suppose that A and B want to sit together. For the sake of argument, we tie A and B together and treat them as one person. The four people are $\fbox{AB}$ CD . Since $\fbox{AB}$ is treated as one person, we have the following possible arrangements:

$\fbox{AB}$ CD , $\fbox{AB}$ DC , C $\fbox{AB}$ D , D $\fbox{AB}$ C , CD $\fbox{AB}$ , DC $\fbox{AB}$

Note that there are six more such permutations because A and B could also be tied in the order BA. And they are:

$\fbox{BA}$ CD , $\fbox{BA}$ DC , C $\fbox{BA}$ D , D $\fbox{BA}$ C , CD $\fbox{BA}$ , DC $\fbox{BA}$

So altogether there are 12 different permutations.

Let us now do the problem using the multiplication axiom.

After we tie two of the people together and treat them as one person, we can say we have only three people. The multiplication axiom tells us that three people can be seated in 3! ways. Since two people can be tied together 2! ways, there are 3!2! = 12 different arrangements.

Example 5.3.6

You have 4 math books and 5 history books to put on a shelf that has 5 slots. In how many ways can the books be shelved if the first three slots are filled with math books and the next two slots are filled with history books?

Solution

We first do the problem using the multiplication axiom.

Since the math books go in the first three slots, there are 4 choices for the first slot, 3 for the second and 2 for the third. The fourth slot requires a history book, and has five choices. Once that choice is made, there are 4 history books left, and therefore, 4 choices for the last slot. The choices are shown below:

4

3

2

5

4

Therefore, the number of permutations are 4 · 3 · 2 · 5 · 4 = 480. Alternately, we can see that 4 · 3 · 2 is really same as 4P3, and 5 · 4 is 5P2. So the answer can be written as (4P3) (5P2) = 480.

Clearly, this makes sense. For every permutation of three math books placed in the first three slots, there are 5P2 permutations of history books that can be placed in the last two slots. Hence the multiplication axiom applies, and we have the answer (4P3) (5P2). We summarize.

Permutations: A permutation of a set of elements is an ordered arrangement where each element is used once.
Factorial: n! = n(n − 1)(n − 2)(n − 3)···3 · 2 · 1. Where n is a natural number. 0! = 1
Permutations of n Objects Taken r at a Time: nPr = n(n − 1)(n − 2)(n − 3)···(n − r + 1), or nPr = 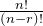$\frac{n!}{(n-r)!}$ . Where n and r are natural numbers.

Circular Permutations and Permutations with Similar Elements

In this section we will address the following two problems.

In how many different ways can five people be seated in a circle?
In how many different ways can the letters of the word MISSISSIPPI be arranged?

The first problem comes under the category of Circular Permutations, and the second under Permutations with Similar Elements.

Circular Permutations

Suppose we have three people named A, B, and C. We have already determined that they can be seated in a straight line in 3! or 6 ways. Our next problem is to see how many ways these people can be seated in a circle. We draw a diagram:

Rendered by QuickLaTeX.com

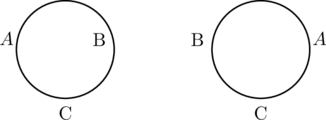
It happens that there are only two ways we can seat three people in a circle. This kind of permutation is called a circular permutation. In such cases, no matter where the first person sits, the permutation is not affected. Each person can shift as many places as they like, and the permutation will not be changed. Imagine the people on a merry-go-round; the rotation of the permutation does not generate a new permutation. So in circular permutations, the first person is considered a place holder, and where he sits does not matter.

Circular Permutations: The number of permutations of n elements in a circle is (n − 1)!

Example 5.3.7

In how many different ways can five people be seated at a circular table?

Solution

We have already determined that the first person is just a place holder. Therefore, there is only one choice for the first spot. We have:

1

4

3

2

1

So the answer is 24.

Example 5.3.8

In how many ways can four couples be seated at a round table if the men and women want to sit alternately?

Solution

We again emphasize that the first person can sit anywhere without affecting the permutation. So there is only one choice for the first spot. Suppose a man sat down first. The chair next to it must belong to a woman, and there are 4 choices. The next chair belongs to a man, so there are three choices and so on. We list the choices below.

1

4

3

2

1

So the answer is 144.

Now we address the second problem.

Permutations with Similar Elements

Let us determine the number of distinguishable permutations of the letters ELEMENT.

Suppose we make all of the letters different by labeling the letters as follows.

E₁LE₂ME₃NT

Since all the letters are now different, there are 7! different permutations.

Let us now look at one such permutation, say:

LE₁ME₂NE₃T

Suppose we form new permutations from this arrangement by only moving the E’s. Clearly, there are 3! or 6 such arrangements. We list them below:

LE₁ME₂NE₃T
LE₁ME₃NE₂T
LE₂ME₁NE₃T
LE₃ME₃NE₁T
LE₃ME₂NE₁T
LE₃ME₁NE₂T

Because the E’s are not different, there is only one arrangement LEMENET and not six. This is true for every permutation.

Let us suppose there are n different permutations of the letters ELEMENT. Then there are n · 3! permutations of the letters E₁LE₂ME₃NT. But we know there are 7! permutations of the letters E₁LE₂ME₃NT. Therefore: n · 3! = 7!

Or n = $\frac{7!}{3!}$ .

This gives us the method we are looking for.

Permutations with Similar Elements:

The number of permutations of n elements taken n at a time, with r₁ elements of one kind, r₂ elements of another kind, and so on, is $\frac{n!}{r_1!r_2!...r_k!}$

Example 5.3.9

Find the number of different permutations of the letters of the word MISSISSIPPI.

Solution

The word MISSISSIPPI has 11 letters. If the letters were all different there would have been 11! different permutations. But MISSISSIPPI has 4 S’s, 4 I’s, and 2 P’s that are alike.

So the answer is $\frac{11!}{4!4!2!}$

Which equals 34,650.

Example 5.3.10

If a coin is tossed six times, how many different outcomes consisting of 4 heads and 2 tails are there?

Solution

Again, we have permutations with similar elements. We are looking for permutations for the letters HHHHTT.

The answer is $\frac{6!}{4!2!} = 15$ .

Example 5.3.11

In how many different ways can 4 nickels, 3 dimes, and 2 quarters be arranged in a row?

Solution

Assuming that all nickels are similar, all dimes are similar, and all quarters are similar, we have permutations with similar elements. Therefore, the answer is:

$\frac{9!}{4!3!2!} = 1260$

Example 5.3.12

A stock broker wants to assign 20 new clients equally to 4 of its salespeople. In how many different ways can this be done?

Solution

This means that each sales person gets 5 clients. The problem can be thought of as an ordered partitions problem. In that case, using the formula we get:

$\frac{20!}{5!5!5!5!} = 11,732,745,024$

We summarize:

Circular Permutations: The number of permutations of n elements in a circle is (n − 1)!
Permutations with Similar Elements: The number of permutations of n elements taken n at a time, with r₁ elements of one kind, r₂ elements of another kind, and so on, such that n = r₁ + r₂ +···+ r_k is

$\frac{n!}{r_1!r_2!···r_k!}$

This is also referred to as ordered partitions.

Practice questions

1. A group of 15 people who are members of a volunteer club wish to choose a chair and a secretary. How many different ways can this be done?

2. How many permutations of the letters of the word SECURITY end in a consonant?

3. In how many different ways can five people be seated in a row if two of them insist on sitting next to each other?

4. In how many ways can 3 English, 3 history, and 2 math books be set on a shelf, if the English books are set on the left, history books in the middle, and math books on the right?

5. Find the number of different permutations of the letters of the word MASSACHUSETTS.

6. If a team plays 10 games, how many different outcomes of 6 wins, and 4 losses are possible?

7. You and six other classmates decide to take a group selfie photo:

a. How many different arrangements are possible?

b. How many different arrangements are possible if you insist on being in the middle of the photo?

c. How many different arrangements are possible if one of your friends insists on being at the right of the photo, and two other friends insist on standing beside each other?

License

Icon for the Creative Commons Attribution-ShareAlike 4.0 International License

Mathematics for Public and Occupational Health Professionals Copyright © 2019 by Ian Young is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License, except where otherwise noted.