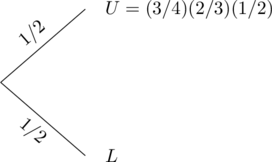7.3. Expected Value and Tree Diagrams
Expected Value
An expected gain or loss in a game of chance is called expected value. The concept of expected value is closely related to a weighted average. Consider the following situations.
1. Suppose you and your friend play a game that consists of rolling a die. Your friend offers you the following deal: If the die shows any number from 1 to 5, he will pay you the face value of the die in dollars, that is, if the die shows a 4, he will pay you $4. But if the die shows a 6, you will have to pay him $18.
Before you play the game you decide to find the expected value. You analyze as follows.
Since a die will show a number from 1 to 6, with an equal probability of 1/6, your chance of winning $1 is 1/6, winning $2 is 1/6, and so on up to the face value of 5. But if the die shows a 6, you will lose $18. You write the expected value.
E = $1(1/6) + $2(1/6) + $3(1/6) + $4(1/6) + $5(1/6) − $18(1/6) = −$0.50
This means that every time you play this game, you can expect to lose 50 cents. In other words, if you play this game 100 times, theoretically you will lose $50. Obviously, it is not in your interest to play.
2. Suppose of the 10 quizzes you took in a course, on eight quizzes you scored 80, and on two you scored 90. You wish to find the average of the 10 quizzes. The average is:
![]()
It should be observed that it will be incorrect to take the average of 80 and 90 because you scored 80 on eight quizzes, and 90 on only two of them. Therefore, you take a “weighted average” of 80 and 90. That is, the average of 8 parts of 80 and 2 parts of 90, which is 82.
In the first situation, to find the expected value, we multiplied each payoff by the probability of its occurrence, and then added up the amounts calculated for all possible cases. In the second example, if we consider our test score a payoff, we did the same. This leads us to the following definition.
Expected Value: If an experiment has the following probability distribution,
| Payoff | x1 x2 x3 ··· xn |
| Probability | p(x1) p(x2) p(x3) ··· p(xn) |
then the expected value of the experiment is:
Expected Value = x1p(x1) + x2p(x2) + x3p(x3) + ··· + xnp(xn)
Example 7.3.1
| Number of Children | 3 | 2 | 1 | 0 |
| Probability | 0.12 | 0.50 | 0.20 | 0.20 |
So on average, there are 1.56 children to a family.
Example 7.3.2
Example 7.3.3
Example 7.3.4
Probability using Tree Diagrams
As we have already seen, tree diagrams play an important role in solving probability problems. A tree diagram helps us not only to visualize but also to list all possible outcomes in a systematic fashion. Furthermore, when we list various outcomes of an experiment and their corresponding probabilities on a tree diagram, we gain a better understanding of when probabilities are multiplied and when they are added. The meanings of the words “and” and “or” become clear when we learn to multiply probabilities horizontally across branches, and add probabilities vertically down the tree.
Although tree diagrams are not practical in situations where the possible outcomes become large, they are a significant tool in breaking the problem down in a schematic way. We consider some examples that may seem difficult at first, but with the help of a tree diagram, they can easily be solved.
Example 7.3.5
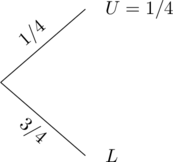
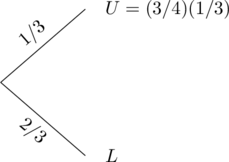
Let U be the event that the door has been unlocked and L be the event that the door has not been unlocked. We illustrate with a tree diagram.
|
|
First Try |
|
|
Second Try |
|
|
Third Try |
Example 7.3.6
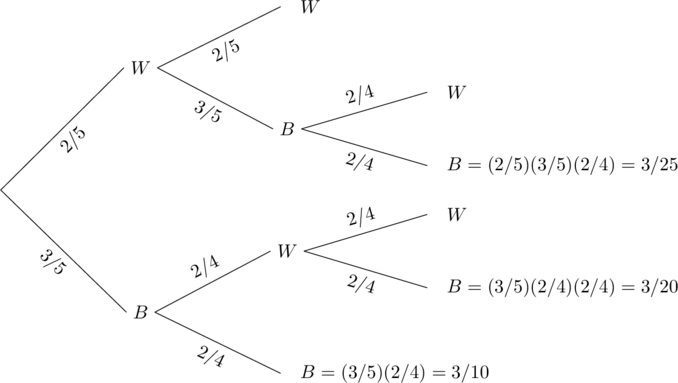
Example 7.3.7
Practice questions
1. In a European country, 20% of the families have three children, 40% have two children, 30% have one child, and 10% have no children. On average, how many children are there to a family?
2. A local community center plans to raise money by raffling a $500 gift card. A total of 3000 tickets are sold at $1 each. Find the expected value of the winnings for a person who buys a ticket in the raffle.
3. A $1 lottery ticket offers a grand prize of $10,000; 10 runner-up prizes each paying $1000; 100 third-place prizes each paying $100; and 1,000 fourth-place prizes each paying $10. Find the expected value of entering this contest if 1 million tickets are sold.
4. A game involves drawing a single card from a standard deck of 52 cards. One receives 75 cents for an ace, 25 cents for a king, and 5 cents for a red card that is neither an ace nor a king. If the cost of each draw is 15 cents, what is the expected value of the game?
5. A basketball player has an 80% chance of making a basket on a free throw. If he makes the basket on the first throw, he has a 90% chance of making it on the second. However, if he misses on the first try, there is only a 70% chance he will make it on the second. If he gets two free throws, what is the probability that he will make at least one of them?
6. A die is rolled until a one (1) shows. What is the probability that a one will show in at most four rolls?
7. You forget to set your alarm 60% of the time. If you hear your alarm, you will turn it off and go back to sleep 20% of the time. Even if you do get up on time, you will be late getting ready about 30% of the time. Under these circumstances, what is the probability that you will be late to class in the morning?
8. Your friend wants to take the Ontario Real Estate License exam, which has a pass rate of about 60%. If a person fails the exam, their success rate improves to about 70% on the second try, and 75% on the third try. What is the probability that your friend will pass the exam in at most three tries?