1.5. Exponents and Scientific Notation
Exponents
Exponent review: an or BaseExponent
| Exponential notation | Example |
| Base Exponent | |
| an= a ∙ a ∙ a ∙ a … a | 24 = 2 ∙ 2 ∙ 2 ∙ 2 = 16 |
| Read “a to the nth” or “the nth power of a.” | Read “2 to the 4th.” |
Properties of exponents:
| Name | Rule | Example |
| Product rule | ||
| Quotient rule | ||
| Power rule |
|
|
| Negative exponent a-n | ||
| Zero exponent a0 | ||
| One exponent a1 | ||
| Fractional exponent |
- Product rule: when multiplying two powers with the same base, keep the base and add the exponents.
am an = am + n an or BaseExponent
| Example: | 23 22 = (2 · 2 · 2) (2 · 2) = 25 = 32 | |
| Or | 23 22 = 23 + 2 = 25 = 32 | A short cut, am an = am + n |
- Quotient rule: when dividing two powers with the same base, keep the base and subtract the exponents.
![]()
| Example: | ||
| Or | A short cut, |
This law can also show that why a0 = 1 (zero exponent a0): ![]()
- Power rule: when raising an expression to a power, we multiply each exponent inside the parentheses by the power outside the parentheses.
(am)n = amn, (am · bn)p = amp bnp, ![]()
| Example: | (43)2 = (43) (43) = (4 · 4 · 4) (4 · 4 · 4) = 46 = 4096 | |
| Or | (43)2 = 43 ∙ 2 = 46 = 4096 | A short cut, (am)n = amn |
| Example: | (2 · 3)2 = (2 · 3) (2 · 3) = 6 ∙ 6 = 36 | |
| Or | (2 · 3)2 = 22 32 = 4 ∙ 9 = 36 | A short cut , (a · b)n = an bn |
| Example: | ||
| Or | A short cut, |
- Negative exponent: a negative exponent is the reciprocal of the number with a positive exponent.
![]() ,
, ![]() a−n is the reciprocal of an.
a−n is the reciprocal of an.
| Example: | ||
| Example: |
- Fractional exponent: a fractional exponent is a different way of writing a radical (i.e. root) sign. The base is first taken to the exponent of m, then the nth root is found to obtain the power.
![]()
| Example: |
Example 1.5.1
Simplify (do not leave negative exponents in the answer).
| 1) |
|
| 2) |
|
| 3) |
|
| 4) |
|
| 5) |
|
| 6) |
|
| 7) |
|
| 8) |
|
| 9) |
|
| 10) |
Simplifying Exponential Expressions
- Remove parentheses using “power rule” if necessary. (am bn)p = amp bnp
- Regroup coefficients and variables.
- Use “product rule” and “quotient rule”. am an = am + n ,
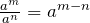
- Simplify.
- Use the “negative exponent” rule to make all exponents positive if necessary.
Example 1.5.2
Simplify.
| 1) |
||
| Remove brackets. | ||
| Regroup coefficients and variables. | ||
| Simplify. | ||
| Make exponent positive. |
| 2) |
||
| Remove brackets. | ||
| Regroup coefficients and variables. | ||
| Simplify. |
Example 1.5.3
Evaluate for a = 2, b = 1, c = -1.
| 1) |
| 2) |
Substitute 2 for a and 1 for b, |
| 3) |
Substitute 2 for a and 1 for b, and -1 for c. |
Scientific Notation
Scientific notation is a special format to concisely express very large and small numbers.
Example:
300,000,000 = 3 × 108 m/sec. The speed of light.
0.00000000000000000016 = 1.6 × 10-19 C. An electron.
Scientific notation: a product of a number between 1 and 10 and a power of 10.
| Scientific notation | Example |
| N × 10±n | 1 ≤ N < 10 | 67504.3 = 6.75043 × 104 | |
| n – integer | Standard form | Scientific notation | |
Writing a number in scientific notation:
| Step | Example |
|
0.0079 37213000 |
|
n = 3 n = 7 |
|
0.0079 = 7.9 × 10-3 3 places to the right. |
|
37213000. = 3.7213 × 107 7 places to the left. |
Example 1.5.4
Write in scientific notation.
1) 2340000 = 2340000. = 2.34× 106
6 places to the left, × 10n
2) 0.000000439 = 4.39 × 10-7
7 places to the right, × 10-n
Example 1.5.5
Write in standard (or ordinary) form.
1) 6.4275 × 104 = 64275
2) 2.9 × 10-3 = 0.0029
Practice questions
1. Evaluate:
a. 4x2 + 5y, for x = 1, y = 4
b. (2a)3 – 3b, for a = 5, b = 6
2. Simplify (do not leave negative exponents in the answer):
a. (-92)1
b. y4 y3
c. ![]()
d. 13a-1
e. (3a2 · b3)4
f. ![]()
g. ![]()
3. Write in scientific notation:
a. 45,600,000
b. 0.00000523
4. Write in standard (or ordinary) form:
a. 3.578 × 103
b. 4.3 × 10-5

