Independent Events
In the previous section, we considered conditional probabilities. In some examples, the probability of an event changed when additional information was provided. For instance, the probability of obtaining a king from a deck of cards changed from 4/52 to 4/12 when we were given the condition that a face card had already shown. This is not always the case. The additional information may or may not alter the probability of the event. For example consider the following example.
A card is drawn from a deck. Find the following probabilities:
a. The card is a king.
b. The card is a king given that a red card has shown.
Solution
a. Clearly, P(The card is a king) = 4/52 = 1/13.
b. To find P(The card is a king | A red card has shown), we reason as follows:
Since a red card has shown, there are only 26 possibilities. Of the 26 red cards, there are two kings. Therefore:
P(The card is a king | A red card has shown) = 2/26 = 1/13.
The reader should observe that in the above example:
P(The card is a king | A red card has shown) = P(The card is a king)
In other words, the additional information, a red card has shown, did not affect the probability of obtaining a king. Whenever the probability of an event E is not affected by the occurrence of another event F, and vice versa, we say that the two events E and F are independent. This leads to the following definition.
Two events E and F are independent if and only if at least one of the following two conditions is true:
1. 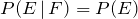
or
2. 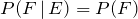
If the events are not independent, then they are dependent. We can test for independence with the following formula.
Test for Independence
Two Events E and F are independent if and only if 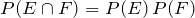
The table below shows the distribution of colour-blind people by gender.
|
Male (M) |
Female (F) |
Total |
| Colour-Blind (C) |
6 |
1 |
7 |
| Not Colour-Blind (N) |
46 |
47 |
93 |
| Total |
52 |
48 |
100 |
Where M represents male, F represents female, C represents colour-blind, and N not colour-blind. Use the independence test to determine whether the events colour-blind and male are independent.
Solution
According to the test,
C and
M are independent if and only if
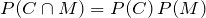
.
and
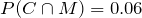
Clearly
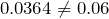
. Therefore, the two events are not independent. We may say they are dependent.
In a survey of 100 adults, 45 owned a home, and 55 did not. Of the 45 who owned a home, 9 had diabetes, and of the 55 who did not, 11 had diabetes. Are the events “owning a home” and “having diabetes” independent?
Solution
Let H be the event that an adult owns a home, and D the event that an adult had diabetes. We have:
In order for two events to be independent, we must have:
Since
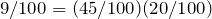
, the two events “owning a home” and “having diabetes” are independent.
A coin is tossed three times, and the events E, F and G are defined as follows:
E: The coin shows a head on the first toss.
F: At least two heads appear.
G: Heads appear in two successive tosses.
Determine whether the following events are independent:
a. E and F b. F and G c. E and G
Solution
To make things easier, we list the sample space, the events, their intersections and the corresponding probabilities:
S = {HHH , HHT , HTH , HTT , THH , THT , TTH , TTT}
E = {HHH , HHT , HTH , HTT},
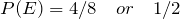
F = {HHH , HHT , HTH , THH},
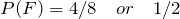
G = {HHT , THH},
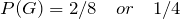

= {HHH , HHT , HTH},


= {HHT , THH},
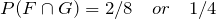
 = {HHT},
= {HHT}, 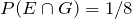
a. In order for E and F to be independent, we must have:
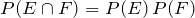
.
But
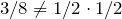
Therefore, E and F are not independent.
b. F and G will be independent if:
Since
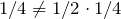
,
F and
G are not independent.
c. We look at
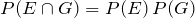
:
Therefore, E and G are independent events.
The probability that Jaime will visit his aunt in Montreal this year is 0.30, and the probability that he will go river rafting on the Ottawa river is 0.50. If the two events are independent, what is the probability that Jaime will do both?
Solution
Let A be the event that Jaime will visit his aunt this year, and R be the event that he will go river rafting.
We are given
P(
A) = 0.30 and
P(
R) = 0.50, and we want to find
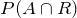
.
Since we are told that the events A and R are independent:
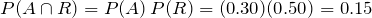
.
Given P(B | A) = 0.4. If A and B are independent, find P(B).
Solution
If A and B are independent, then by definition P(B | A) = P(B).
Therefore, P(B) = 0.4
Given
P(
A) = 0.7,
P(
B |
A) = 0.5. Find
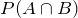
.
Solution
By definition
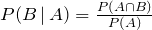
Substituting, we have:
Therefore,
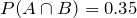
Given
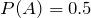
,
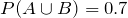
, if
A and
B are independent, find
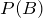
.
Solution
The addition rule states that:
Since
A and
B are independent,
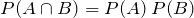
We substitute for
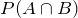
in the addition formula and get:
By letting
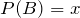
, and substituting values, we get:
Therefore,
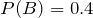
.
Practice questions
1. In a survey of 100 people, 40 were casual drinkers, and 60 did not drink. Of the ones who drank, 10 had minor headaches. Of the non-drinkers, 5 had minor headaches. Are the events “drinkers” and “had headaches” independent?
2. Suppose that 80% of people wear seat belts, and 5% of people quit smoking last year. If 4% of the people who wear seat belts quit smoking, are the events wearing a seat belt and quitting smoking independent?
3. If 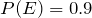 ,
, 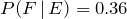 , and E and F are independent, find
, and E and F are independent, find 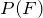 .
.
4. John’s probability of passing Data Management is 40%, and Linda’s probability of passing the same course is 70%. If the two events are independent, find the following probabilities:
a. P (both of them will pass the course)
b. P (at least one of them will pass the course)
5. The table below shows the distribution of employees in a company that reported a previous workplace injury based on their years of working experience at the company.
|
Less than 10 years of experience (L) |
10 or more years of experience (E) |
Total |
| Did not report a workplace injury (N) |
300 |
100 |
400 |
| Reported a workplace injury (Y) |
150 |
50 |
200 |
|
450 |
150 |
600 |
Use this table to determine the following probabilities:
a. 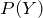
b. 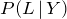
c. 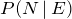
d. Are the events L and Y independent?
6. Given 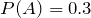 ,
, 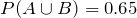 , if A and B are independent, find
, if A and B are independent, find 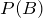 .
.
![]()
![]()
![]()
![]() = {HHT},
= {HHT}, ![]()
![]() ,
, ![]() , and E and F are independent, find
, and E and F are independent, find ![]() .
.![]()
![]()
![]()
![]() ,
, ![]() , if A and B are independent, find
, if A and B are independent, find ![]() .
.
