10.2 Evans’ Root Locus Construction Rules – Introduction

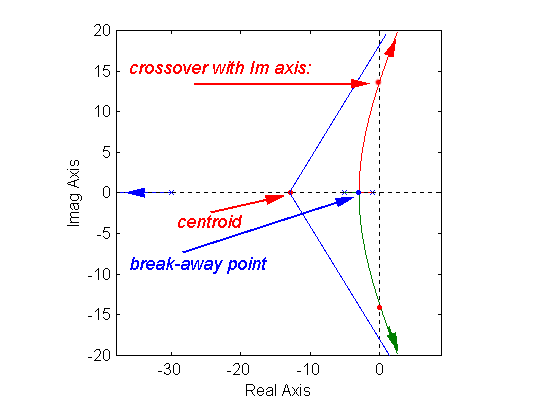
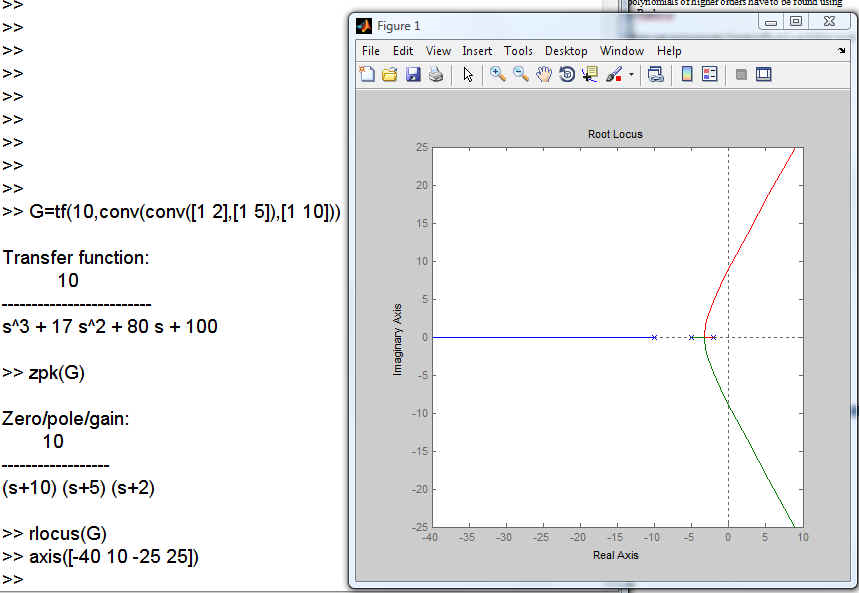
To use analytic techniques to solve Equation 10‑2 for [latex]0

Construction rules developed by Evans dealt with:

Rule 1: Beginning and end of Root Locus plot, symmetry;

Rule 2: Points on the Real axis;

Rule 3: Asymptotic angles and centroid;

Rule 4: Break-away (break-in) points;

Rule 5: Crossovers with Imaginary axis;

Rule 6: Angles of departure (arrival) from/to complex poles (zeros).

Evans also established how to determine the Proportional Gain used in the closed loop system operation that corresponds to any particular point [latex]s^*[/latex] on the Root Locus by:

• Preparing an accurate Root Locus plot
• Using the magnitude criterion to evaluate the gain at the point [latex]s^*[/latex]

[latex]1+K^*G(s^*)=0\rightarrow K^*=\frac{1}{|G(s^*)|}[/latex]

NOTE: In Matlab, to plot Root Locus plots and to evaluate the gains on the plots we will use the rlocus.m and rlocfind.m subroutines. Figure 10‑3 shows where the starting points of RL are, the crossover with the Imaginary axis, asymptotes, centroid and break-away point on RL.

As a MATLAB example, consider a unit feedback closed loop control system under Proportional Gain, where the process transfer function G(s) is as shown below. The Root Locus plot is obtained by MATLAB and shown in Figure 10‑4.

[latex]G(s)=\frac{10}{s^3+17s^2+80s+100}=\frac{10}{(s+10)(s+5)(s+2)}[/latex]