Chapter 9
9.3 Proportional + Derivative Control
Consider again the example from Chapter 9.2, where G(s) was described by Equation 9‑3. Assume the closed loop system has a PD Control implemented. You are or will be, be familiar with the PD Control from Lab 2. Replace the Proportional Controller in Figure 9‑9 with the PD Controller described by the following transfer function:
| [latex]G_{PD}(s)=K_p\cdot(K_d s +1)[/latex] or | |
| [latex]G_{PD}(s)=K_p\cdot(\tau_d s +1)[/latex] | Equation 9-6 |
The adjustable derivative variable is referred to either as the Derivative Gain, [latex]K_d[/latex], or the Derivative Time Constant, [latex]\tau_d[/latex]. The closed loop system transfer function is then as follows:
| [latex]G_{clPD}(s)=\frac{K_p(1+K_d s)G(s)}{1+K_p(1+K_d s)G(s)} = \frac{10K_p(1+K_d s)}{s^4 + 15s^3 + 54s^2 + (30+10K_p K_d)s+(4+10K_p)}[/latex] | Equation 9-7 |
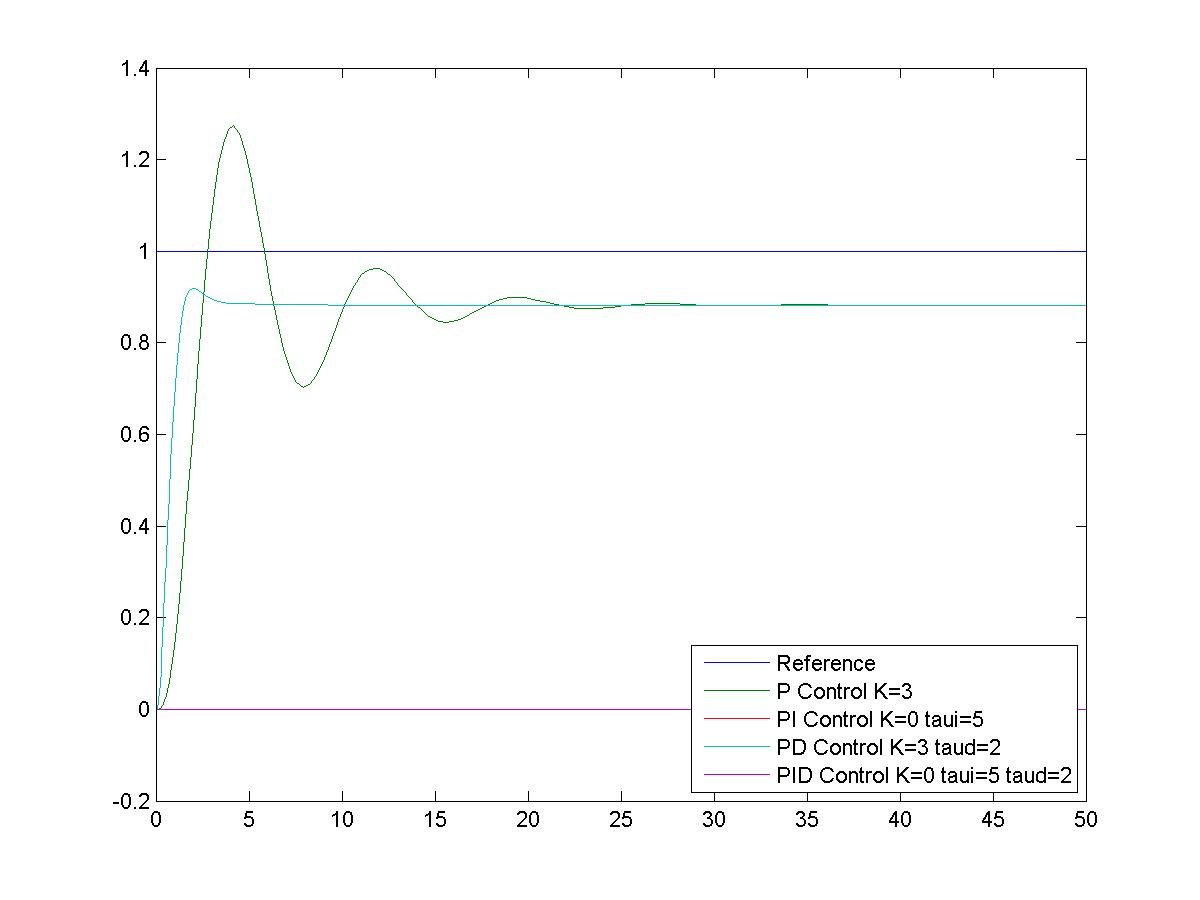
Let’s assume the value of the Derivative Gain [latex]K_d[/latex] = 2 seconds. The critical gain can be calculated from the Routh-Hurwitz Criterion as [latex]K_{crit}=33.55[/latex] and the resulting frequency of marginal oscillations is calculated as [latex]\omega_{osc}=6.84[/latex] rad/sec. Figure 9‑12 shows the effect of Proportional + Derivative Control on the closed loop response of this system – with the same controller gain value, the oscillations are greatly reduced but there is no effect on the steady state tracking (error).
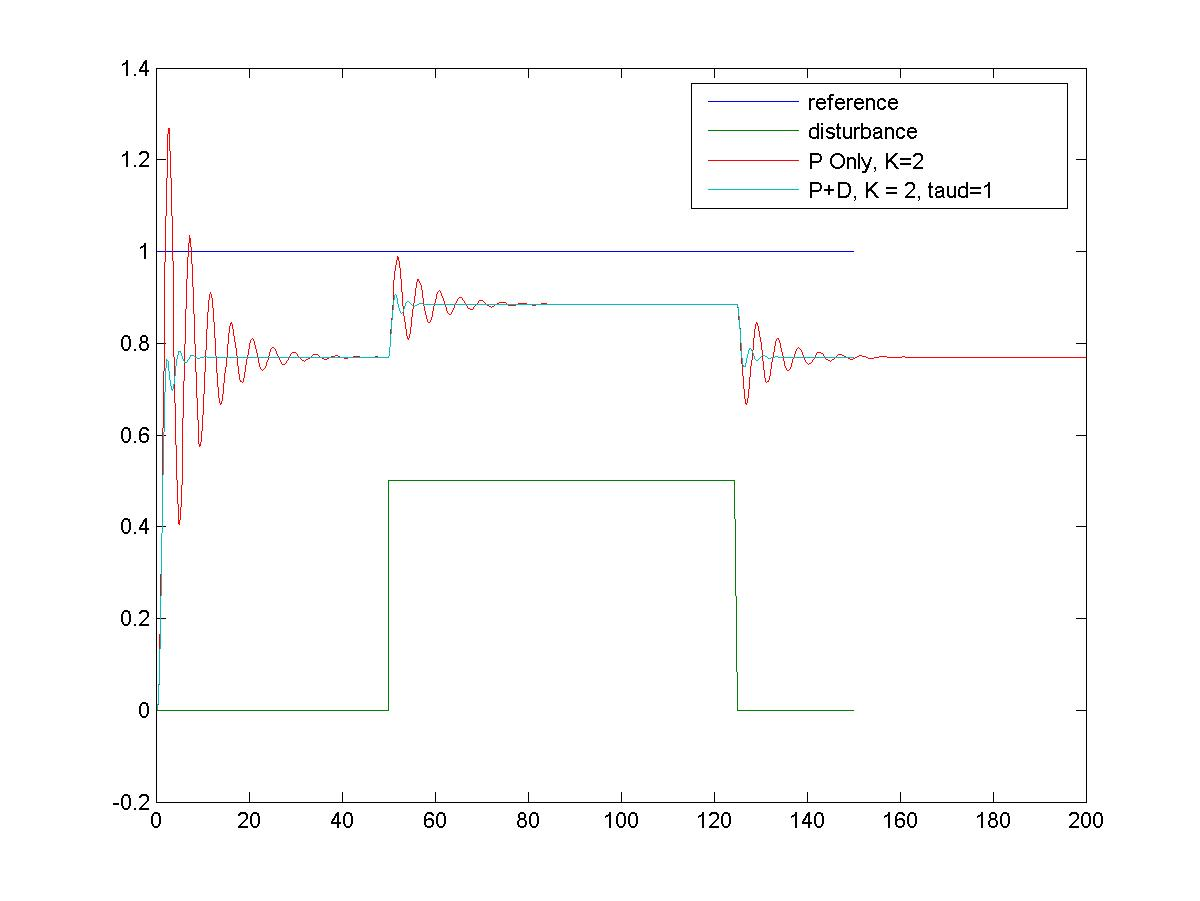
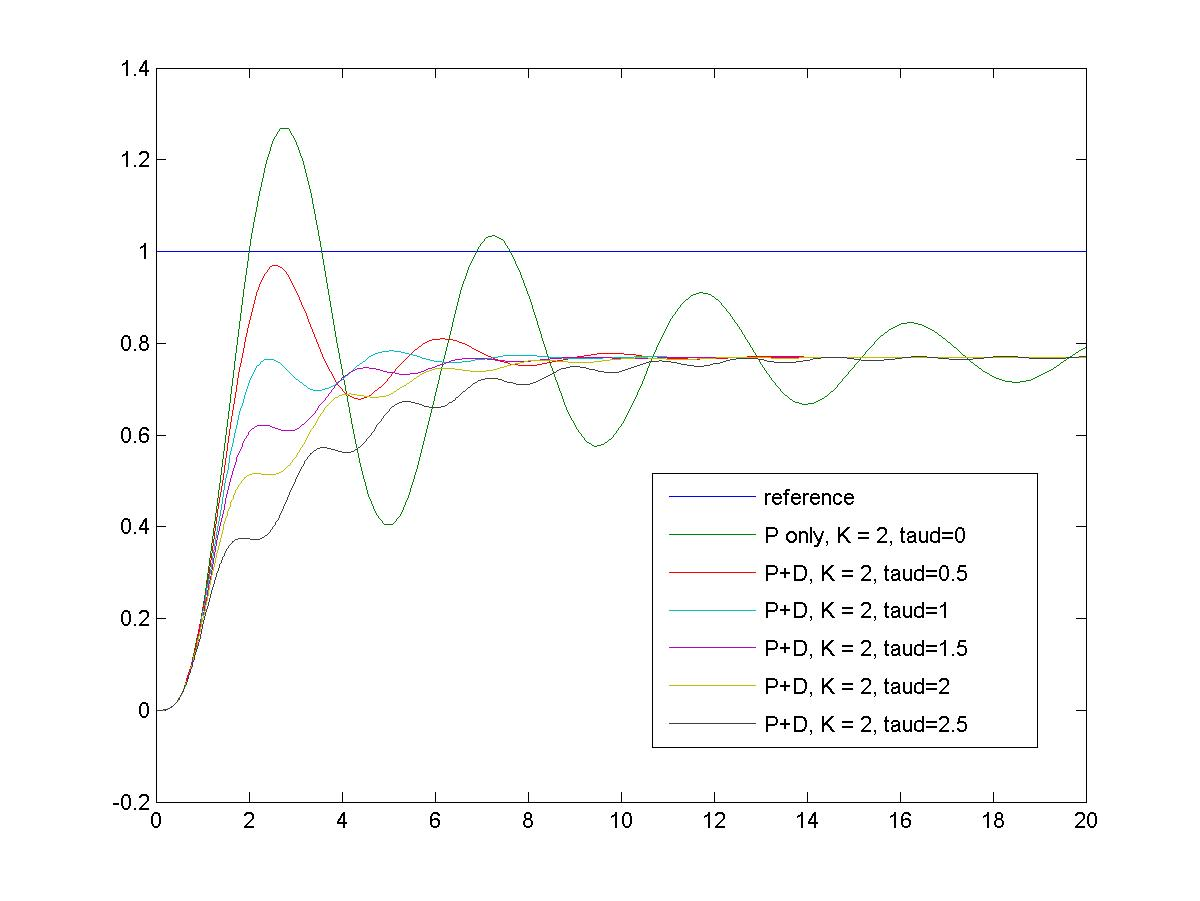
Figure 9‑13 shows the same system response in presence of a disturbance. As expected, there is no effect on the steady state controller effectiveness in reducing the effect of the disturbance, but the transient effect of the disturbance signal is reduced – fewer oscillations. Figure 9‑14 shows how the changing value of the Derivative Time Constant (the same as Derivative Gain [latex]K_d[/latex]) affects the system closed loop response. The larger the value of the Derivative Time Constant (or Derivative Gain) the stronger the Derivative effect – hence fewer oscillations.
9.3.1 Proportional + Derivative Control in Presence of Noise
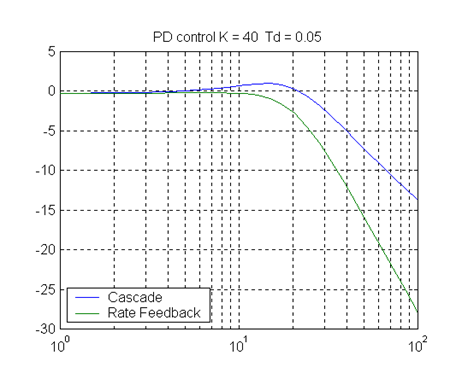
Let’s consider now the effect of using a Derivative Control on the system closed loop frequency response – specifically, its bandwidth. Figure 9‑15 shows the closed loop frequency response of the system under PD Control vs. the closed loop frequency response of the system under P + Rate Feedback Control.
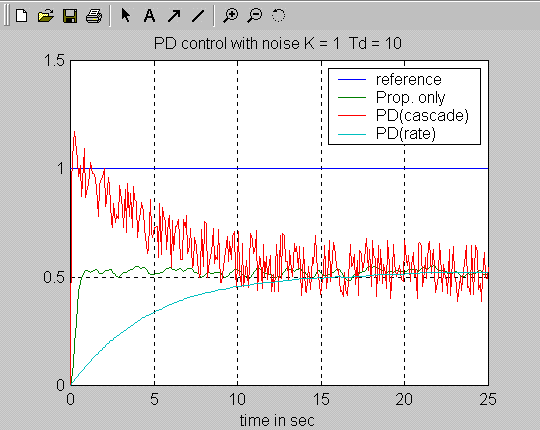
As seen in Figure 9‑15, the Derivative term in frequency domain is characterized by a constant +20dB/dec slope on the magnitude plot. Thus, the closed loop zero in PD configuration increases the bandwidth of the closed loop system, as shown in Figure 9‑15, thus reducing the noise attenuation. This effect does not occur with the P + Rate Feedback configuration, as that configuration does not have a zero. The effect of these differences in the closed loop bandwidth is illustrated in Figure 9‑16 which shows a comparison of the responses of a closed loop system under PD Control vs. P + Rate Feedback Control when the system operates in an environment subject to noise.
As can be seen, PD Control significantly amplifies the noise and as such, it is not recommended in environments where noise is expected. If the controller is to operate in a noisy environment, the P+Rate Feedback scheme is a better option. However, if the reduction of the Derivative effect is not sufficient, there is one more possibility – the Derivative effect can be limited by replacing the PD part of the controller transfer function with the so-called Lead Network – see more discussion of it in the PID Control section.
9.3.2 Summary of Proportional + Derivative Control Attributes
Steady state tracking:
- Derivative action has no effect on the system type and on steady state errors
Dynamic Tracking:
- Derivative can be implemented as PD term in cascade, or as rate feedback. The rate feedback configuration will not introduce a zero to the system and will be slower, but also without an additional overshoot.
- High proportional gain – undesirable (strong) control effort – may saturate the controller
- Derivative is implemented by introducing a zero to the system, which has a high-pass filter characteristic. Thus, Derivative Mode increases the system bandwidth and makes it more susceptible to noise, as higher frequency components are not well attenuated
- Typically, too much of the Derivative action results in a jittery response and vibrations. Rate feedback is not as noisy as the cascade configuration.

