9.7 Examples

9.7.1 Example

Consider a closed loop unit feedback system operating initially under Proportional Control where the process transfer function G(s) is as follows:

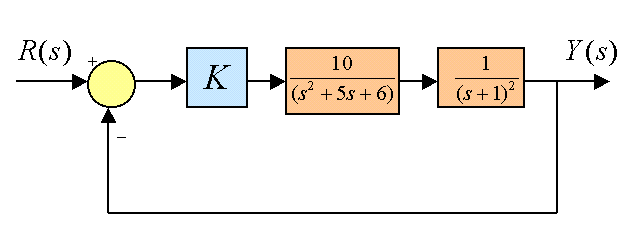
Part 1. Find the stability range, and assume the operating gain such that the Gain Margin = 2.

Part 2. Next, replace the gain with a parallel structure of the PID Controller, with the settings for the Derivative Time Constant [latex]\tau_d =2[/latex] seconds and for the Integral Time Constant [latex]\tau_i =10[/latex]seconds. Fine-tune the PID Controller by simulations.

Consider again the system from Example 7.3.17 and Example 8.7.14, only now the P+Rate Feedback and PI+ Rate Feedback are replaced with a series configuration of a PID Controller, as shown.

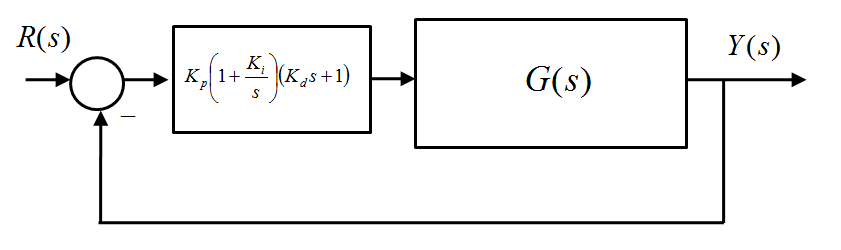
G(s) process transfer function remains the same as before:

[latex]G(s)=\frac{1}{s^2+7s+5}[/latex]

All gain values are kept exactly the same as you determined them in those two previous examples:

[latex]K_p=40.78[/latex], [latex]K_d=0.0245[/latex] and [latex]K_i=0.7[/latex].  How different will be the PID system closed loop transfer function from the P+Rate and PI+Rate? How different will the system step response be? Will the difference be significant? Briefly justify your answers.