Chapter 4
4.3 Step response specifications – Definitions
4.3.1 Percent Overshoot
Maximum Overshoot is defined as:
| [latex]MO = y_{max} - y_{ss}[/latex] | Equation 4‑1 |
Percent Overshoot is defined as:
| [latex]PO = \frac{y_{max} - y_{ss}}{y_{ss}} \cdot 100[/latex]% | Equation 4‑2 |
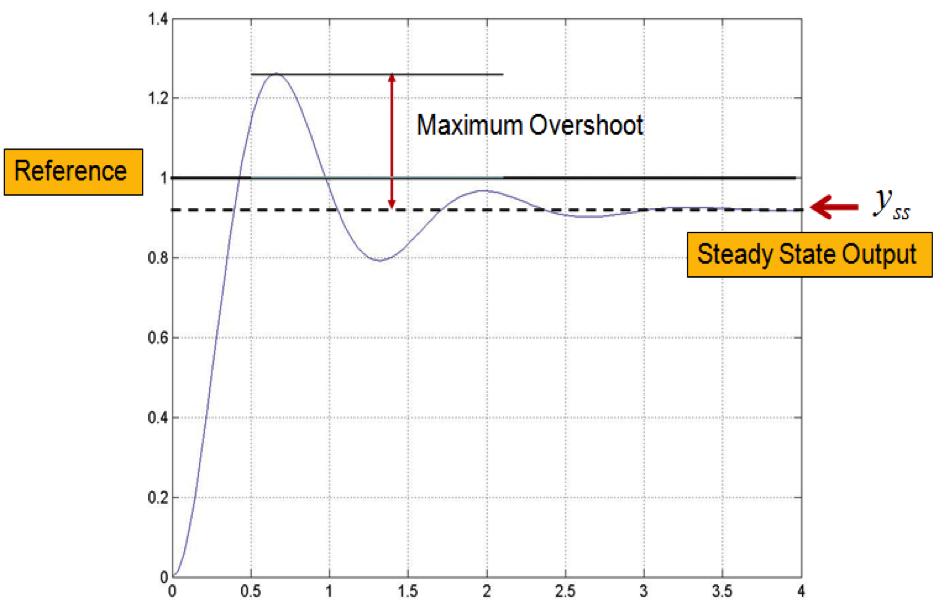
Note that while the constant reference signal (which can be referred to as [latex]r_{ss}[/latex]) in Figure 4‑2 is shown as unit (1), in fact, it does not have to be that, and can be any value.
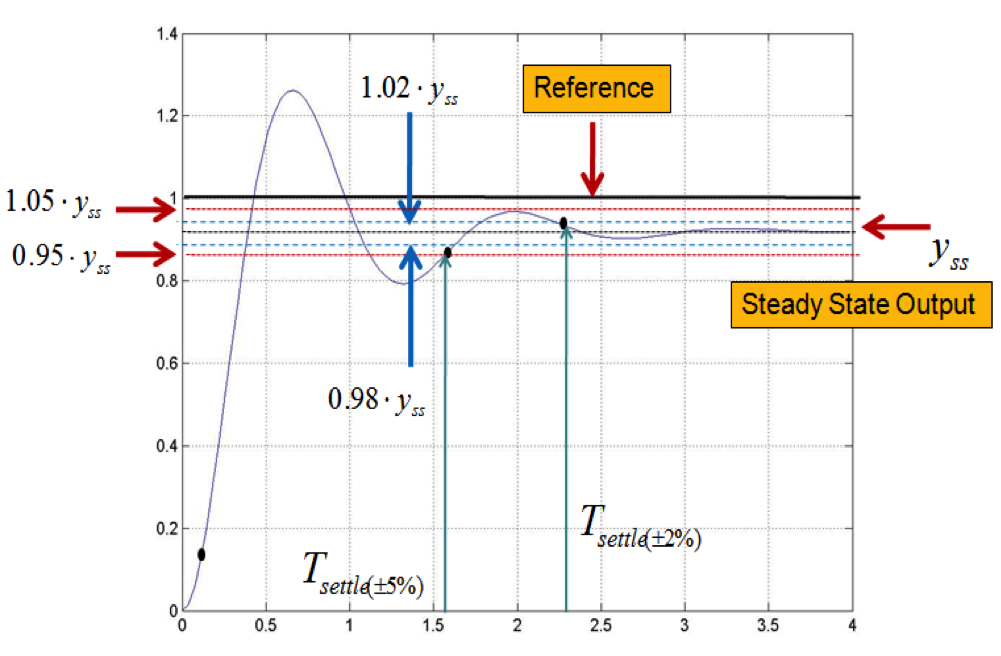
4.3.2 Settling Time
The Settling Time [latex]T_{settle}[/latex] is defined, as shown in Figure 4‑3, as either [latex]T_{settle(\pm 5 \%)}[/latex] – within 5% of the steady state value, or [latex]T_{settle(\pm 2\%)}[/latex] – within 2% of the steady state value.
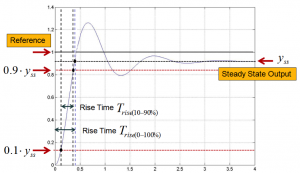
4.3.3 Rise Time
The Rise Time [latex]T_{rise}[/latex] is defined, as shown in Figure 4‑4, as either calculated as time from 10% to 90% of the steady state value of the output, [latex]y_{ss}[/latex], or from 0 to 100% of the steady state value of the output, [latex]y_{ss}[/latex].
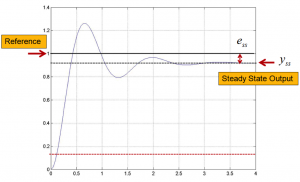
4.3.4 Steady State Error
The Steady State Error [latex]e_{ss}[/latex] is defined, as shown in Figure 4‑5 and Equation 4‑3:
[latex]e_{ss} = r_{ss} - y_{ss}\%[/latex]
[latex]e_{ss\%} = \frac{r_{ss} - y_{ss}}{r_{ss}} \cdot 100\%[/latex]