14.5 Concept of Mapping

Consider a map (function) [latex]F(s)[/latex]:

[latex]F(s)=[/latex] [latex]\frac{s+5}{(s+1)(s+3)}[/latex]

The map (function) has [latex]3[/latex] singularities: a zero at [latex]-5[/latex], and two poles, at [latex]-1[/latex] and [latex]-3[/latex].

Consider an arbitrarily closed contour [latex]\sigma[/latex] in the s-plane, traversed clockwise (CW), so that it does not go through any singularities of [latex]F(s)[/latex]. Let [latex]Z[/latex] be a number of zeros of [latex]F(s)[/latex] inside the [latex]\sigma[/latex]-contour, and [latex]P[/latex] be a number of poles of [latex]F(s)[/latex] inside the [latex]\sigma[/latex] -contour. Mapping the [latex]\sigma[/latex] -contour into the [latex]F(s)[/latex] plane will result in a closed [latex]\Gamma[/latex] -contour. Let [latex]N[/latex] be a number of clockwise (CW) encirclements of the resulting [latex]\Gamma[/latex]-contour around the origin of the [latex]F(s)[/latex]-plane.

14.5.1 Case 1

Let the [latex]\sigma[/latex]-contour be so chosen that Z = 0 and P = 0, i.e. there are no singularities of [latex]F(s)[/latex] inside the [latex]\sigma[/latex] – contour. Note that the resulting [latex]\Gamma[/latex] -contour in the [latex]F(s)[/latex]-plane does not encircle the origin of [latex]F(s)[/latex]-plane, i.e. N = 0.

14.5.2 Case 2

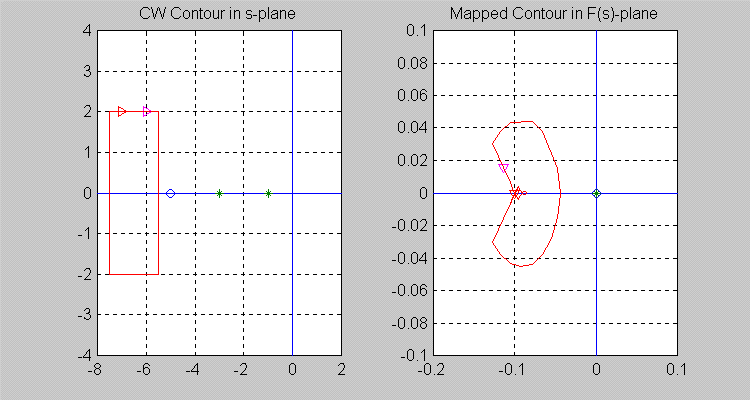
Next, let the [latex]\sigma[/latex] -contour be so chosen that [latex]Z =1[/latex] and P = [latex]0[/latex], i.e. there is one zero of [latex]F(s)[/latex] inside the [latex]\sigma[/latex] -contour. Note that the resulting [latex]\sigma[/latex]-contour in the [latex]F(s)[/latex]-plane encircles the origin of [latex]F(s)[/latex]-plane once in a clockwise (CW) direction, i.e. N =[latex]+1[/latex].

14.5.3 Case 3

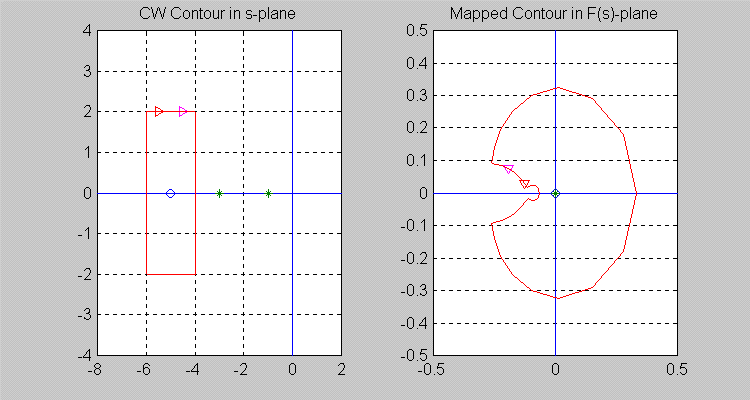
Next, let the [latex]\sigma[/latex]-contour be so chosen that [latex]Z =0[/latex] and [latex]P = 1[/latex], i.e. there is one pole of [latex]F(s)[/latex] inside the [latex]\sigma[/latex]-contour. Note that the resulting [latex]\Gamma[/latex] -contour in the [latex]F(s)[/latex]-plane encircles the origin of [latex]F(s)[/latex]-plane once in a counter-clockwise (CCW) direction, i.e. [latex]N = -1[/latex].

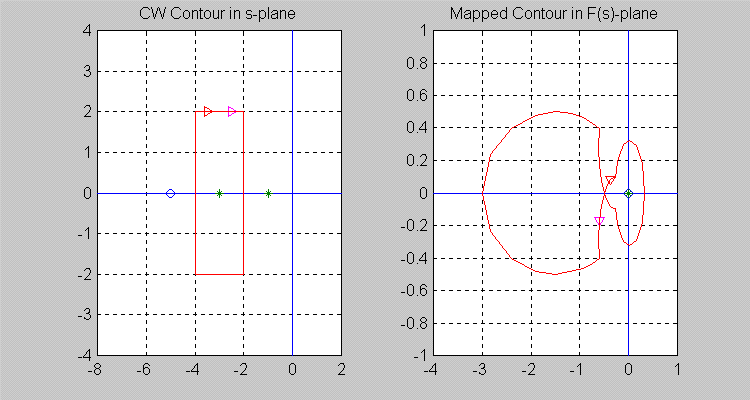
14.5.4 Case 4

Next, let the [latex]\sigma[/latex]-contour be so chosen that [latex]Z = 1[/latex] and [latex]P = 1[/latex], i.e. there is one zero and one pole of [latex]F(s)[/latex] inside the [latex]\sigma[/latex] -contour. Note that the resulting [latex]\Gamma[/latex]-contour in the [latex]F(s)[/latex]-plane does not encircle the origin of [latex]F(s)[/latex]-plane, i.e. [latex]N = 0.[/latex]

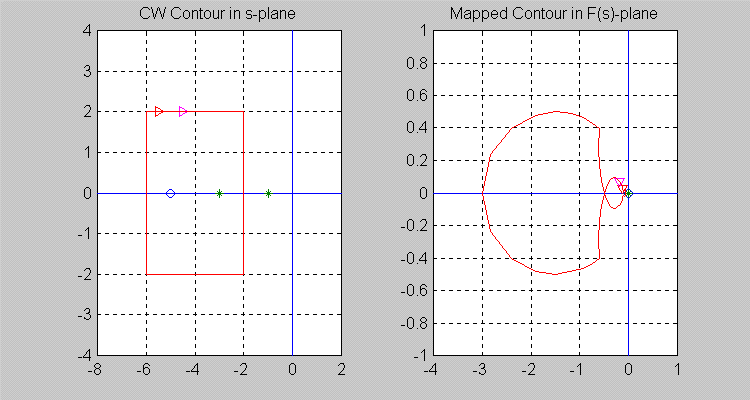
14.5.5 Case 5

Next, let the [latex]\sigma[/latex]-contour be so chosen that [latex]Z = 0[/latex] and [latex]P = 2[/latex], i.e. there are two poles of [latex]F(s)[/latex] inside the [latex]\sigma[/latex]-contour. Note that the resulting [latex]\Gamma[/latex]-contour in the [latex]F(s)[/latex]-plane encircles the origin of [latex]F(s)[/latex]-plane twice in a counter-clockwise (CCW) direction, i.e. [latex]N = -2.[/latex]

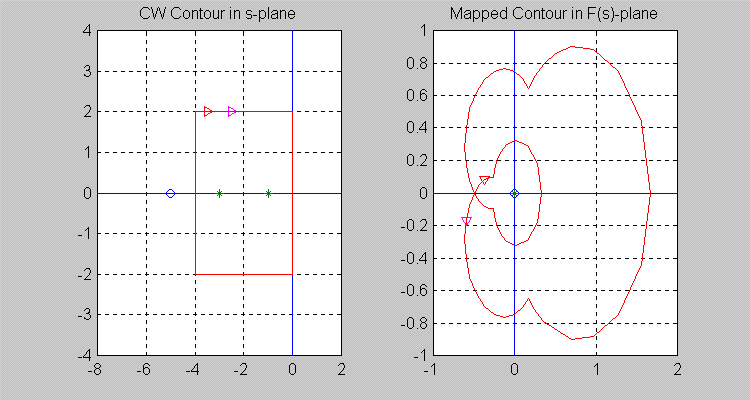
14.5.6 Case 6

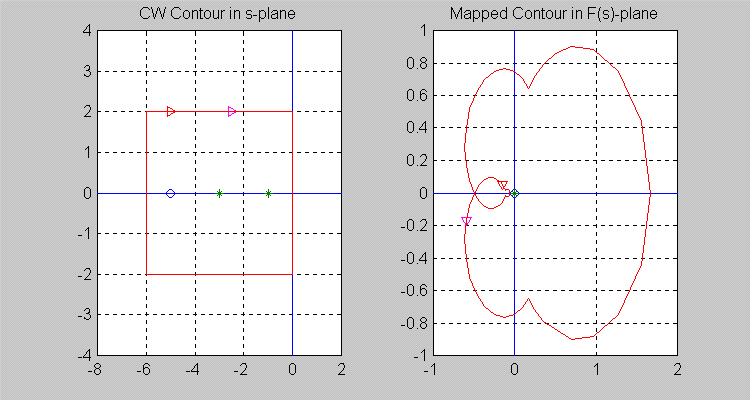
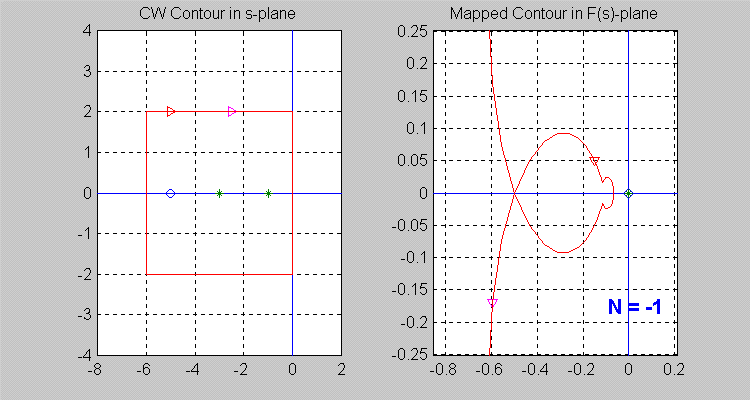
Next, let the [latex]\sigma[/latex]-contour be so chosen that [latex]Z = 1[/latex] and [latex]P = 2[/latex], i.e. there is [latex]1[/latex]  zero and [latex]2[/latex] poles of [latex]F(s)[/latex] inside the [latex]\sigma[/latex] -contour. The area of the origin may not be very visible, so see a zoomed version in Error! Reference source not found. Note that the resulting [latex]\Gamma[/latex]-contour in the [latex]F(s)[/latex]-plane encircles the origin of [latex]F(s)[/latex]-plane once in a counter-clockwise (CCW) direction, i.e. [latex]N = -1[/latex].