Chapter 10
10.4 Evans Root Locus Construction Rule # 2: Segments of Root Locus on Real Axis
This Rule deals with points on the Real axis. Consider the angle criterion:
| [latex]\angle G(s) = 180^{\circ} \pm n\cdot360^{\circ}[/latex] | |
| [latex]\angle(s-z_1)+\angle(s-z_2)+...+\angle(s-z_m)-...[/latex] | |
| [latex]\angle(s-p_1)-\angle(s-p_2)-...-\angle(s-p_n)=180^{\circ}\pm n360^{\circ}[/latex] | Equation 10-6 |
Take some test points for [latex]s^*[/latex] along the Real axis and see what satisfies the angle criterion.
[latex]\angle G(s^*)=\sum\theta_z - \sum\theta_p[/latex]
Where must Real axis segments of the root locus lie? Rule 2 answers that question.
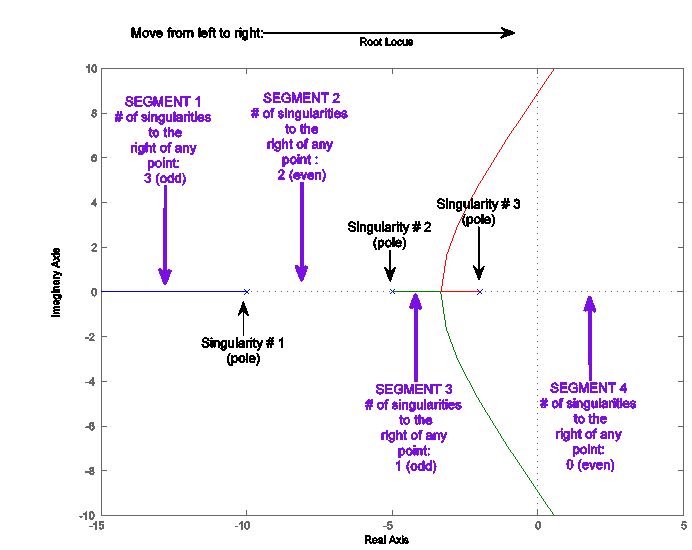
Rule 2: A point s on the Real axis belongs to the root locus if and only if it is to the left of the ODD number of open loop singularities (a singularity is either a pole or a zero).
As an example, consider the RL plot shown in Figure 10‑4, with Real Axis segments as shown in Figure 10‑5.