Chapter 5
5.1 Equivalent Unit Feedback Loop
Consider a typical single feedback loop system:
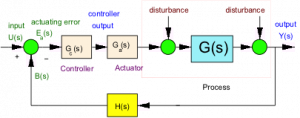
In most cases, the system will be non-unit feedback. For example, y(t) may be a temperature signal, and b(t) will be a voltage signal out of a thermocouple (sensor). The input signal u(t) will also be a voltage signal. It is pointless to make comparisons between u(t) and y(t). Let us introduce the reference signal, r(t) (a desired level of output, and not a physical quantity), and the so-called system error, e(t):
|
[latex]e(t) = r(t) - y(t)[/latex] [latex]E(s) = R(s) - Y(s)[/latex] |
Equation 5‑1 |
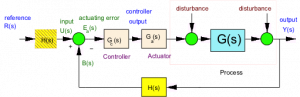
These signals can then be introduced into the system block diagram:
An equivalent unit feedback loop system will be then:
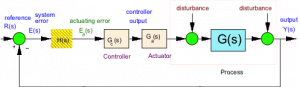
The steady state error analysis can then be performed on the equivalent system, for the system error signal e(t) (or E(s) in Laplace domain), and the reference signal r(t) (or R(s) in Laplace domain). However, in the physical system, the input is u(t) (or U(s) in Laplace domain), and the controller input is the actuating error [latex]e_{a}(t)[/latex] (or [latex]E_{a}(s)[/latex] in Laplace domain). Note that the equivalent unity feedback loop has the “open loop transfer function”, G(s)H(s), in its forward path:
| [latex]\frac{Y(s)}{R(s)} = H(s) \cdot \frac{Y(s)}{U(s)} = H(s) \cdot \frac{G(s)}{1+ G(s)H(s)} = \frac{G(s)H(s)}{1+G(s)H(s)} = \frac{G_{open}(s)}{1+G_{open}(s)}[/latex] |
Equation 5‑2 |

